Bir futbol maçını Trabzonspor 9-5 kazanmıştır.Trabzonun bu maç esnasında geriye düşmüş olma olasılığı kaçtır?
1001 / 2002 buldum doğru mu?
1/2 diyorsunuz yani kodunuzu ve mantığınızı açıklarmısınız ben de 1/4 buldum ama emin değilim
Doğru cevabı bilmiyorum
Başta string değişkenleri ve permutations() fonksiyonu ile yapmaya çalıştım ama nedenini anlamadığım şekilde çok yavaş çalıştığını gördüm. Ardından kodun daha hızlı çalışması için permutations() fonksiyonunu kullanmak yerine sayısal değerler ile product() fonksiyonundan aldığım çıktıyı filter() fonksiyonu ile filtre ettim. Dolayısıyla programı optimize yapmak için sayısal değer kullandım ve bu da kodun okununurluğu zorlaştırdı. Sonuç olarak, anlamadığınız yer olursa sorabilirsiniz. (1 değerleri Trabzonspor’un attığı, 0 değeri ise karşı takımın attığı golleri temil ediyor.)
from itertools import product
def geriye_dusmus_mu(dizilis: list) -> bool:
for i in range(len(dizilis)):
gecici_dizilis = dizilis[:i]
if sum(gecici_dizilis) < len(gecici_dizilis) / 2:
return True
return False
olasiliklar = list(filter(lambda x: sum(x) == 9, product(range(2), repeat=14)))
geriye_dustugu_olasiliklar = 0
toplam_olasiliklar = 0
for dizilis in olasiliklar:
if geriye_dusmus_mu(dizilis):
print(dizilis)
geriye_dustugu_olasiliklar += 1
toplam_olasiliklar += 1
print("TÜM OLASILIKLAR : {}".format(toplam_olasiliklar))
print("GERİYE DÜŞTÜĞÜ OLASILIKLAR : {0}".format(geriye_dustugu_olasiliklar))
Kod kısaca Trabzonspor’un ve karşı takımın attığı gollerin permutasyon ile 14 elemanlı listeler döndürmesini sağlıyor. geriye_dusmus_mu() fonksiyonu ile de Trabzonspor’un (1 değerini temsil ediyor) Geride olup olmadığını teyit ediyorum.
Galiba yazdığınız kod toplam 14gol üzerinden gidiyor ama kaybeden takımın 5gol attığını kontrol etmiyor.Bundan dolayı cevap%50geldi diye düşünüyorum
Zaten burda toplamın 9 olduğunu sorguluyorum. TS’a 1, karşı takıma da 0 değer verdiğim için her bir sıralamanın toplamı 9 çıkıyor. Zaten çıktıya da bakarsanız karşı takımın attığı goller (0 lar) her bir dizilişte 5 tane. Yani gol sayısında bir sıkıntı yok. Bence kendi yazdığınız kodu burda paylaşırsanız daha hızlı ilerleyebiliriz.
Ben bi şey yazdım ama bakar mısın?
Şuan okuldayım eve geçince paylaşırım
Sizin yaptığınızla benim mantığım aynı kodlar farklı sadece 1/4 çıktısı veriyor dimi?
İ ile k nın yeri değişecek sadece
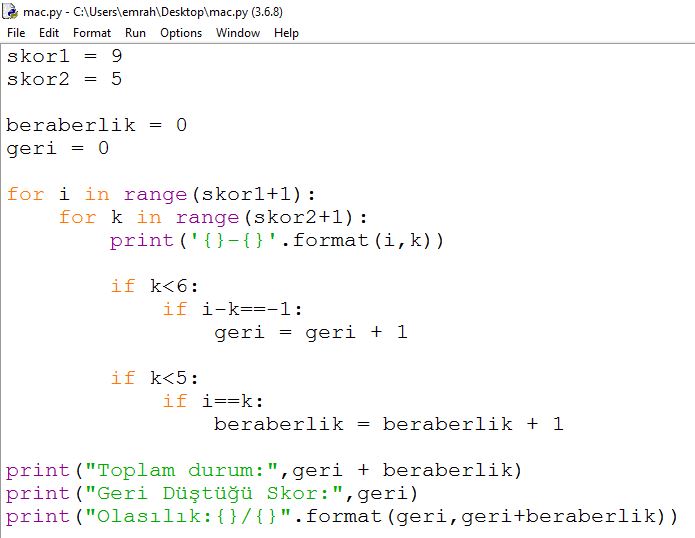
Geride olduğu skorları sayıp, tüm skorlara böldüm.15/60 sonucu veriyor.Ama şöyle bir sorun var 0-1 dan sonra 0-2 olduğunda zaten gerideydi, tekrar geriye düşme durumu yok.Bunu gözardı ettim bunun için de bir kontrol yazman lazım.
Evet i ile k yer değişecek.Onu yanlış yazmışım.Aradaki skor farkı 2 ve üzerine çıkıyorsa zaten geridedir tekrar geriye düşme durumu yok.Bunun için if deyimiyle araya kontrol koyman lazım.
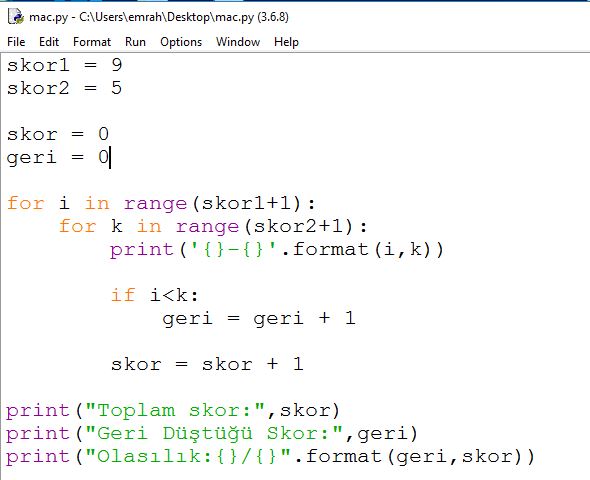
import itertools
liste=itertools.product(range(0,10),repeat=2)
tüm_durum=[]
istenen_durum=[]
for i in liste:
if i[0]<6:
tüm_durum.append(i)
if i[0]>i[1]:
istenen_durum.append(i)
print(tüm_durum)
print(istenen_durum)
olasılık=len(istenen_durum)/len(tüm_durum)
print(olasılık)sizin çözümünüz daha mantıklı büyük ihtimalle de doğru cevap
Benim hatam Örneğin:1 -0 öne geçebilir ama bu 1 kere olmuyorki birden fazla durumda bu olay söz konusu hepsini belirlemek lazım ve diğer arkadaşın da söylediği gibi 1-0 önde olduğu maçtada 2-0 öne geçmiş olabilir.Sizin kodunuz tüm durumları kontrol ediyor.
İlginç olan cevabın 1/2 olması
Olayı çözdüm
Rakibin öne geçme durumları:
0-1,1-2,2-3,3-4,4-5 (5 durum)
Trabzonun önde olduğu durumları olasılığa almıyoruz zaten önde beraberlik olabilir.
Rakibin önde olduğu durumları da almıyoruz beraberlik olabilir.
Beraberlik durumunda bu olay gerçekleşebilir.
Onlar da
0-0,1-1,2-2,3-3,4-4 (5 durum)
5-5 i almıyoruz öne geçme ihtimali yok maç zaten 9-5 bitmiş.
Olası durum : 5
Toplam durum : 10
5/10 : 1/2
Oncelikle tekrarsiz permutasyon lazim:
def permutations_with_duplicates(bags):
bagf = list(filter(lambda bag: bag[1] > 0, bags))
for i in range(len(bagf)):
subs = permutations_with_duplicates(bagf[:i] + [(bagf[i][0], bagf[i][1] - 1)] + bagf[i+1:])
for sub in subs:
yield (bagf[i][0],) + sub
if len(bagf) == 0: yield ()
permutations_with_duplicates = lambda bags: (lambda bagf: [()] if len(bagf) == 0 else ((bagf[i][0],) + sub for i in range(len(bagf)) for sub in permutations_with_duplicates(bagf[:i] + [(bagf[i][0], bagf[i][1] - 1)] + bagf[i+1:])))(list(filter(lambda bag: bag[1] > 0, bags)))
assert sorted(list(permutations_with_duplicates([('a', 2), ('b', 2)]))) == sorted([('a', 'a', 'b', 'b'), ('a', 'b', 'a', 'b'), ('a', 'b', 'b', 'a'), ('b', 'a', 'a', 'b'), ('b', 'a', 'b', 'a'), ('b', 'b', 'a', 'a')])
assert sorted(map("".join, permutations_with_duplicates([('a', 1), ('b', 2), ('c', 1)]))) == ['abbc', 'abcb', 'acbb', 'babc', 'bacb', 'bbac', 'bbca', 'bcab', 'bcba', 'cabb', 'cbab', 'cbba']
Gerisine bakiyorum…
inits = lambda xs: [] if len(xs) == 0 else [[xs[0]]] + list(map(lambda xt: [xs[0]] + xt, inits(xs[1:])))
print((lambda perms: len(list(filter(lambda x:x, map(lambda sums: any(map(lambda sum_: sum_ < 0, sums)), map(lambda inits_: list(map(sum, inits_)), map(inits, perms)))))) / len(perms)) (list(permutations_with_duplicates([(+1, 9), (-1, 5)]))))
0.5 (1001/2002)
Sunu su sekilde yazarken aklimda (map.map) sum veya filter (any (<0)) diyebildigin Haskell vardi… Python’da boyle oluyor.
Mantik da su:
permutations_with_duplicates([(+1, 9), (-1, 5)]) → 9 gol atilip 5 gol yiyilen butun maclar (2002 tane)
map inits permutasyonlar → maclarin her golden sonraki gol durumu (2002×14 tane)
map sum durumlar = map sum.inits permutasyonlar → durumlardaki gol farki (2002×14 tane)
filter (any (<0)) farklar → gol farkinin herhangi bir durumda negatif oldugu maclar (1001×14 tane)
from itertools import product
geri_kalma_olasilik = lambda atilan, yenilen: (len(siralamalar := list(filter(lambda x: sum(x) == atilan, product(range(2), repeat=atilan + yenilen)))) / sum(any(sum(gecici_dizilis := dizilis[:idx]) < len(gecici_dizilis) / 2 for idx in range(len(dizilis))) for dizilis in siralamalar)) ** -1
print(geri_kalma_olasilik(9, 5))
Üstte yazdığımı kısalttım. Ayrıca farklı gol sayıları için de çalışmasını sağladım.
Matematiğim berbat ama şu mantığı kurdum:
Trabzonspor hiç gol atmaz,karşı takım gol atar:
0-1 (1. geri düşme)
Ve Trabzonspor gol atar:
1-1
Döngü devam eder:
1-2, (2. geri düşme)
2-2,
2-3, (3. geri düşme)
3-3,
3-4, (4. geri düşme)
4-4,
4-5, (5. geri düşme)
5-5,
6-5,
7-5,
.
.
.
Yeni bence karşı takımın attığı gol atma sayısı.Yani karşı takım 5 gol attı ise: 100%5=20
Bana göre cevap: %20
Toxide ve aib in çözümlerini incelerseniz mümkün tüm durumları ve şartları sağlayanları göreceksiniz