Merhabalar,
Bir kaç gün önce karşıma çıkan, Mathologer kullanıcı adıyla YouTube’da yayın yapan Burkard Polster’a ait bir videodan bahsetmek istiyorum.
İlgili arkadaşlar için video adresi: https://www.youtube.com/watch?v=qhbuKbxJsk8
Bu videoda Burkard Polster, çarpım tablolarını kullanarak nasıl belli başlı fractalların oluştuğunu bizlere animasyon üzerinden anlatıyor. Animasyonu izlerken, animasyonu tasarlama isteği oluştu ve aşağıda paylaştığım kodlar ortaya çıktı.
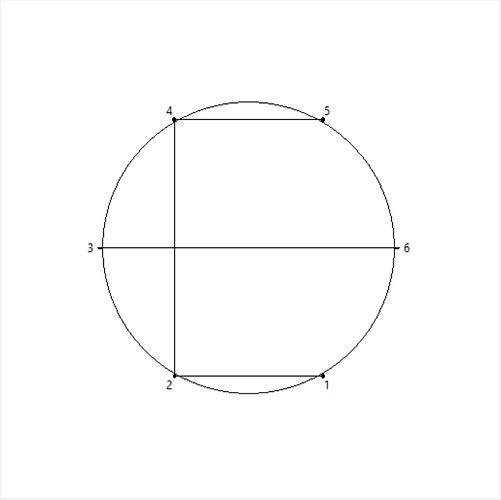
Animasyon bir çember üzerinde gösteriliyor. Mesela aşağıdaki gibi:
Bu çember üzerinde, çemberi eşit parçalara bölen, istediğimiz kadar nokta tanımlayabiliriz değil mi?
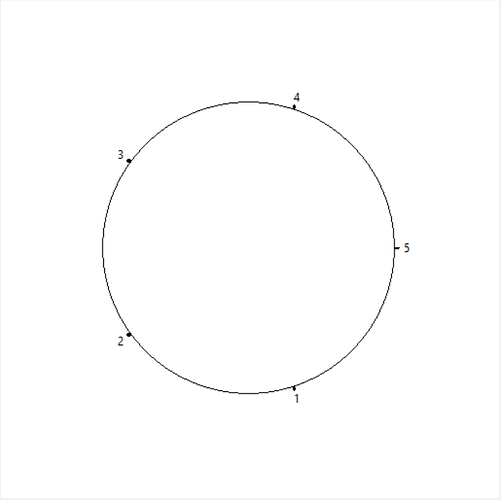
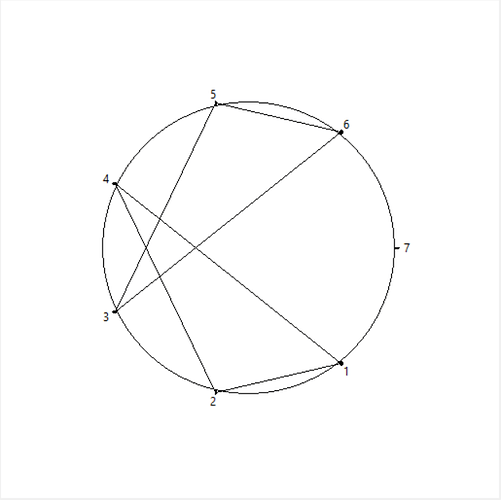
Bir çemberi 5 eşit parçaya bölen 5 adet noktayı mesela şöyle gösterebiliriz.
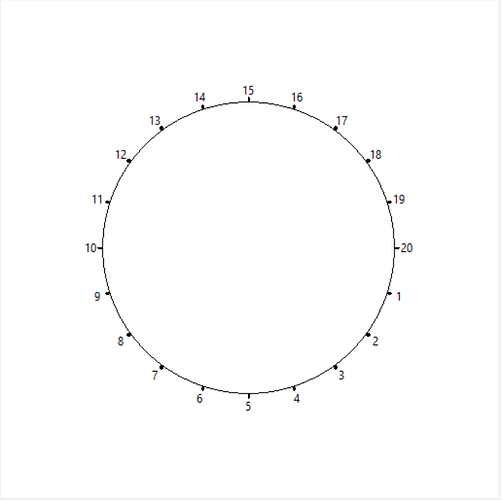
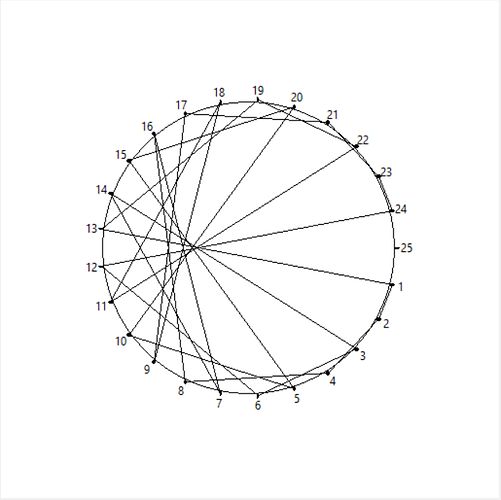
Veya bir çemberi 20 eşit parçaya bölen 20 adet noktayı şöyle gösterebiliriz:
Yukarıda her bir noktanın bir sayıyla gösterildiğini görüyorsunuz.
Şimdi, çemberdeki her bir noktayı çemberdeki başka bir noktayla, bir çarpan yardımıyla bağlayacağız.
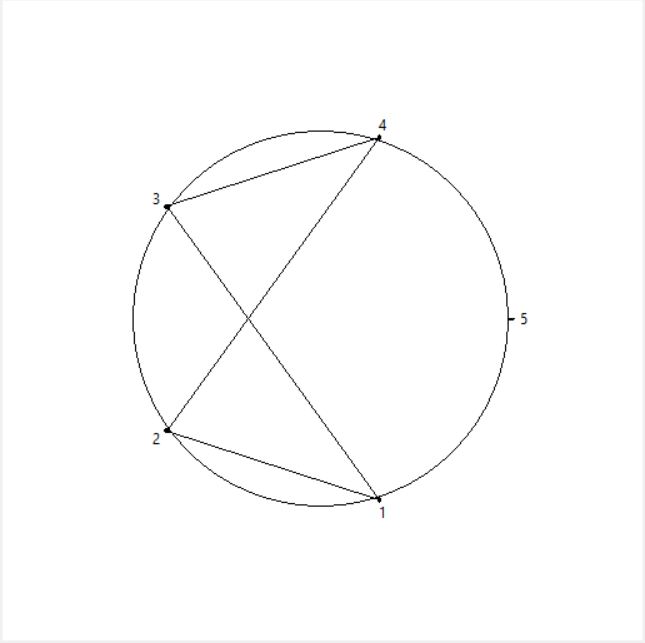
Örneğin 5 tane noktamız olsun. Ve çarpan olarak da 2’yi seçmiş olalım.
- 1’i 2 ile çarparsak sonuç 2 olur. O halde 1’den 2’ye bir çizgi çizilir.
- 2’yi 2 ile çarparsak sonuç 4 olur. 2’den 4’e bir çizgi çizilir.
- 3’ü 2 ile çarparsak sonuç 6 olur. Ama 5 tane noktamız olduğu için,
1,6’yı simgeler. O halde 3’den 1’e bir çizgi çizilir. - 4’ü 2 ile çarparsak sonuç 8 olur. 5 tane noktamız olduğu için, 8’in 5’e bölümünden kalan 3 olur. O halde 4’den 3’e doğru bir çizgi çizilir.
- 5’i 2 ile çarparsak sonuç 10 olur. 5 tane noktamız olduğu için, 10’un 5’e bölümünden kalan 0 olur. O halde 5’den 5’e giden bir çizgi çizilir. (5’den 5’e giden bir çizgi çizemeyiz.)
Sonuç olarak 5 nokta için çarpan 2 olursa, çizgilerin görünümü şu şekilde olacaktır:
6 nokta için çarpan 2 olursa çizgilerin görünümü şu şekilde olur:
7 nokta için çarpan 2 olursa, çizgilerin görünümü şu şekilde olur:
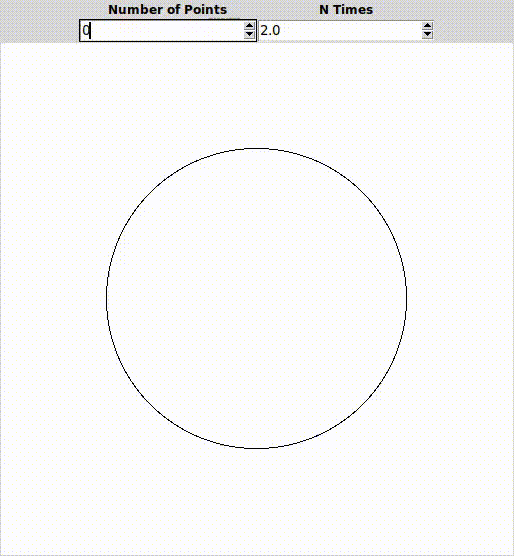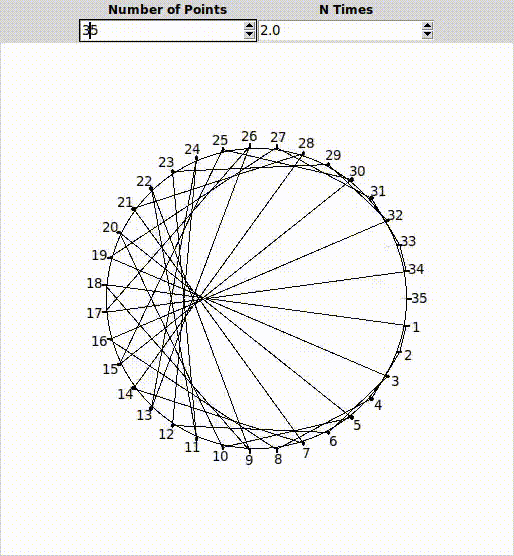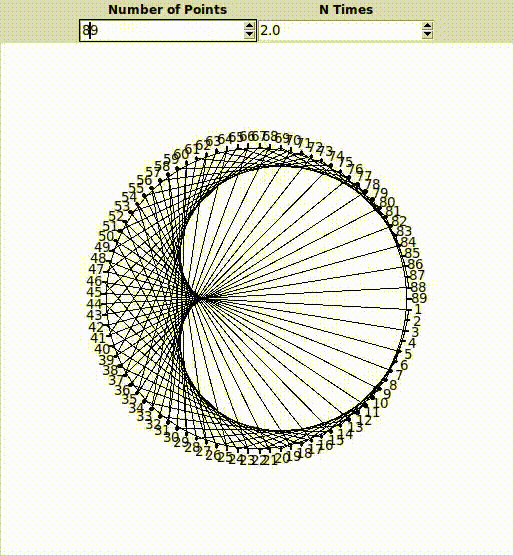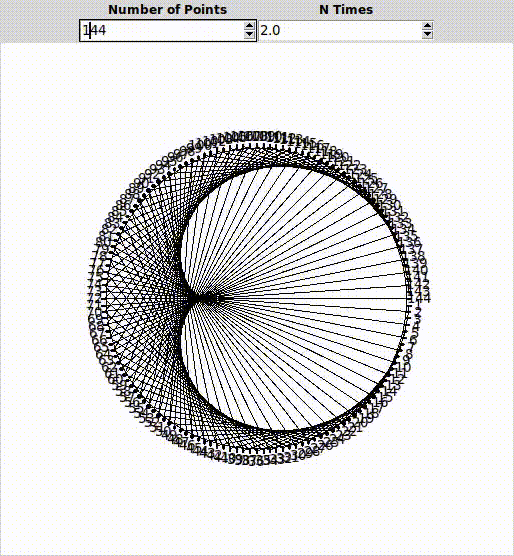
25 nokta için çarpan 2 olursa, çizgilerin görünümü şu şekilde olur:
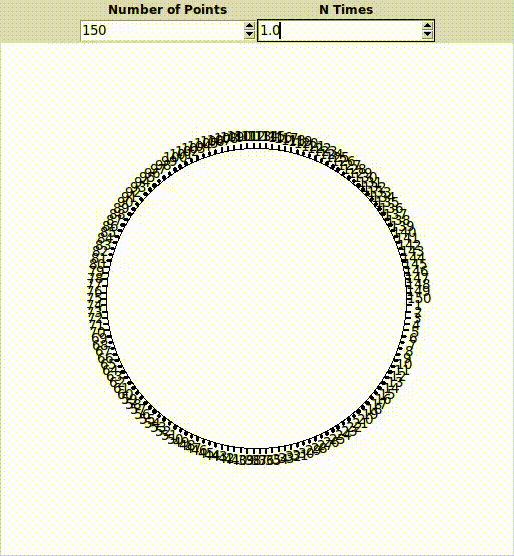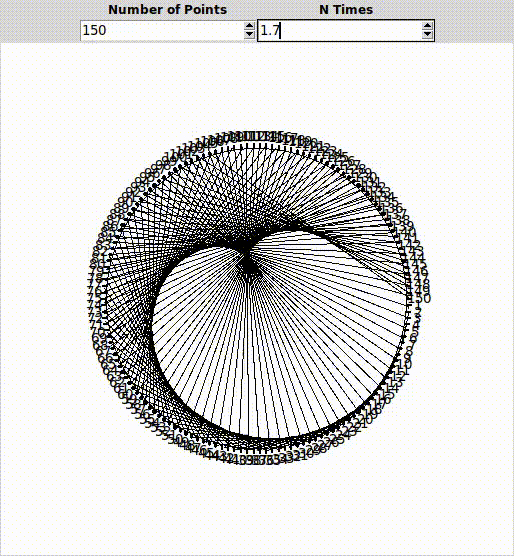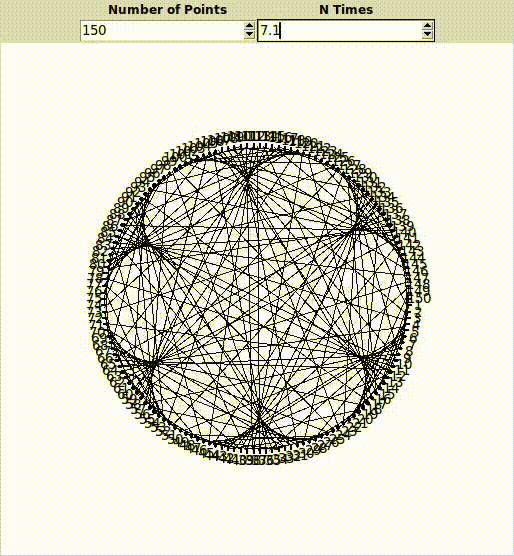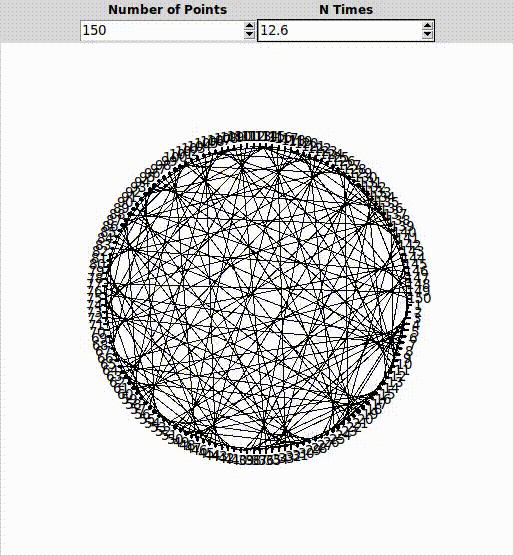
Dikkatinizi çektiyse, nokta sayımızı artırdıkça özel bir şekil oluşmaya başlıyor. Şekil henüz çok belirgin değil. Nokta sayımızı biraz daha artıralım, mesela 100’e çıkartalım:
360’a çıkartalım:
İşte, çarpanın 2 olduğu durumda oluşan bu geometrik şekle “Cardioid” deniyor.
Çarpanın 3 olduğu durumda oluşan geometrik şekle “Nephroid” deniyor.
Bu şekillerin genel ismi de episikloid’tir.
Epicycloid - Wikipedia
In geometry, an epicycloid is a plane curve produced by tracing the path of a chosen point on the circumference of a circle—called an epicycle—which rolls without slipping around a fixed circle.
Çarpan 2.5 olsaydı nasıl olurdu?
Gördüğünüz gibi yarısı Cardioid, yarısı Nephroid olan bir şekil bu.
Cardioid’in oluşumu:
Episikloid’lerin oluşumu:


Kod:
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
import tkinter as tk
from math import cos, sin, radians
class Point(list):
def __init__(self, x: float, y: float, r: float, q: float):
super().__init__(
j + (i * f(radians(q)))
for i in [r, r + 5] for f, j in ([cos, x], [sin, y])
)
def xy(self):
return (self[0] + self[2]) / 2, (self[1] + self[3]) / 2
class Circle(list):
def __init__(self, x: float, y: float, r: float):
super().__init__([x - r, y - r, x + r, y + r])
class Canvas(tk.Canvas):
points = []
def __init__(self, *args, **kwargs):
super().__init__(*args, **kwargs)
self.pack()
self.x = pow(2, 8)
self.y = pow(2, 8)
self.r = 150
self["width"] = self.x * 2
self["height"] = self.y * 2
self.create_oval(Circle(x=self.x, y=self.y, r=self.r))
def create_points(self, n: int, x: int | float):
for i in range(1, n + 1):
p1 = Point(x=self.x, y=self.y, r=self.r, q=i * 360 / n)
p2 = Point(x=self.x, y=self.y, r=self.r, q=((x * i) % n) * 360 / n)
p3 = Point(x=self.x, y=self.y, r=self.r + 10, q=i * 360 / n)
self.points += [self.create_oval(p1, fill="black")]
self.points += [self.create_line(*p1.xy(), *p2.xy())]
self.points += [self.create_text(*p3.xy(), text=i)]
def delete_points(self):
self.delete(self.points)
self.points = []
def change_points(self, n: int, x: int | float):
self.delete_points()
self.create_points(n, x)
class Spinbox(tk.Frame):
def __init__(
self,
text: str,
start: int,
end: int,
step: float,
var: tk.IntVar | tk.DoubleVar,
*args,
**kwargs
):
super().__init__(*args, **kwargs)
self.pack(side="left")
self.var = var
self.label = tk.Label(master=self, text=text, font="Default 9 bold")
self.label.pack()
self.spinbox = tk.Spinbox(
master=self,
from_=start,
to=end,
increment=step,
textvariable=self.var,
)
self.spinbox.pack()
class Window(tk.Tk):
def __init__(self, *args, **kwargs):
super().__init__(*args, **kwargs)
self.frame = tk.Frame(master=self, bg="white")
self.frame.pack()
self.number_of_points = Spinbox(
master=self.frame,
text="Number of Points",
start=0,
end=1000,
step=1,
var=tk.IntVar()
)
self.n_times = Spinbox(
master=self.frame,
text="N Times",
start=1,
end=1000,
step=0.1,
var=tk.DoubleVar()
)
self.canvas = Canvas(master=self, bg="white")
for i in [self.number_of_points, self.n_times]:
i.spinbox["command"] = lambda: self.canvas.change_points(
n=self.number_of_points.var.get(),
x=self.n_times.var.get()
)
i.spinbox.bind(
sequence="<KeyRelease>",
func=lambda event: self.canvas.change_points(
n=self.number_of_points.var.get(),
x=self.n_times.var.get()
)
)
self.mainloop()
if __name__ == "__main__":
Window()