hocam merakımdan soruyorum neden kodları yazarken sonuna [0] ekleyerek yazıyorsunuz ? bir amacı var mı acaba ?
f = quad(func=integrand, a=0, b=radians(10))[0]
buradaki gibi 
:)
quad() fonksiyonu bir tuple verisi dönderiyor. 0. indeksteki değer fonksiyonun a ve b arasındaki integralini veriyor, ikinci değer ise abserror isminde bir değer. Sonuçtaki mutlak hatanın bir tahminidir. Aslında quad fonksiyonu birçok değer dönderebiliyor:
Returns
-------
y : float
The integral of func from `a` to `b`.
abserr : float
An estimate of the absolute error in the result.
infodict : dict
A dictionary containing additional information.
Run scipy.integrate.quad_explain() for more information.
message
A convergence message.
explain
Appended only with 'cos' or 'sin' weighting and infinite
integration limits, it contains an explanation of the codes in
infodict['ierlst']
1 Beğeni
anladım teşekkür ederim
1 Beğeni
Tekrar merhaba,
Uzun zaman oldu ama konuya uygun açıklamalı bir cevap vermiş olalım.
Sizin yazdığınız fonksiyon, daha geleneksel bir yaklaşım. @aib’in dediği gibi sabit bir Δx seçmek yerine n’in alacağı değere göre değişebilecek bir Δx seçebilirsiniz. n’in alacağı değer işlem hızını doğrudan etkiler.
Ayrıca yönteminizde, mesela şöyle bir şey yazmışsınız: for i in range(1,n-1,2): bu ifade x1 için çalışıyor. Sonra, for i in range(2,n-2,2): şu ifade de x2 için çalışıyor. Bu iki ifadeyi ele alacak olursanız, toplam işlem adımı n-3. Ancak dilerseniz işlem adımını da kısaltabilirsiniz.
Aşağıdaki kodu inceleyin isterseniz:
def simpsons(f, n: int, a: int, b: int):
return sum(f(a + (i * d)) + 4 * f(a + ((i + 1) * d)) + f(a + ((i + 2) * d)) for i in range(0, n, 2)) * d / 3 if (d := (b - a) / n) else 0
Yukardaki kodda, Δx, yani d, n’in alacağı değere göre değişecektir. for i in range(0, n, 2) ile de döngü sayısını n/2 yapıyoruz.
Sizin yazdığınız kod, şu formülü esas alıyor:
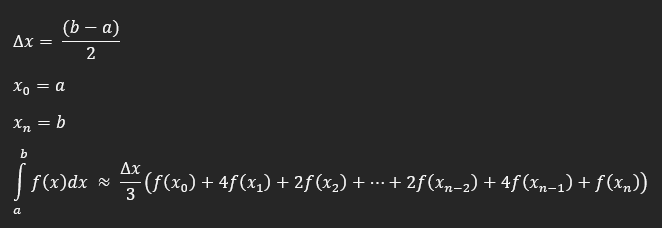
Paylaştığım kod ise aşağıdaki formülü esas alıyor:
İzninizle bu formüldeki ifadeyi nasıl elde ediyoruz adım adım anlatayım:
Şimdi bildiğiniz gibi, Simpsons 1/3 kuralı polinomlarla alakalı bir metod. Ve biz bir sürü polinomun alanını kullanarak, eğrinin alanını kestirmeye çalışıyoruz.
Peki bir polinomun genel formülü nasıldı hatırlayalım:
Şimdi, Simpsons kuralı bize şunu diyor:
f(x) fonksiyonunda tanımlı olan ve aralarında eşit Δx mesafe bulunan ardışık 3 noktayı kesen bir polinomun integrali, f(x) fonksiyonunun o üç noktadaki integraline hemen hemen eşittir.
Yani:
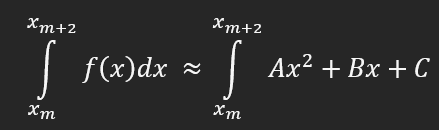
Şimdi, elimizde, koordinatları aşağıdaki gibi olan 3 nokta var:
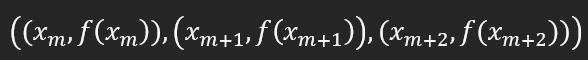
f yerine p yazabiliriz demiştik:
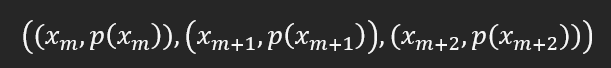
O halde fonksiyonların formülleri de şöyle olmaz mı?
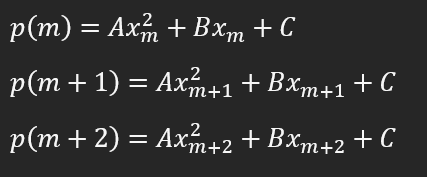
Şimdi, m, m+1 ve m+2 noktalarından geçen polinomun alanını hesaplayacağız. Bir polinomun alanını hesaplamak için türevin tersi bir işlem yapmamız gerekir.
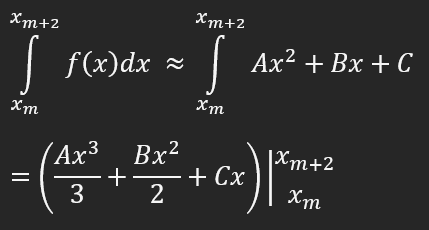
Bu ifadeyi açalım:
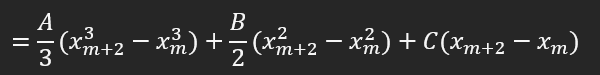
Paydaları eşitleyelim ve üslü sayı eşitlik kurallarını kullanarak bazı ifadeleri açalım:
Son paylaştığım ifadede gruplandırılabilir kısımlar var, onları gruplandırıp yeniden yazalım:
(x_m+2 - x_m) / 6 yerine, Δx / 3 yazabiliriz.
Şimdi bu son ifadeye dikkatinizi verin: Bu ifadedeki 2A(x_m+2)^2 kısmından 1 tane A(x_m+2)^2, 3B(x_m+2)'den de 1 tane B(x_m+2) ve 6C’den 1 tane C alsak A(x_m+2)^2 + B(x_m+2) + C ifadesini oluşturmuş oluruz değil mi?
A(x_m+2)^2 + B(x_m+2) + C gördüğüm yere f(x_m+2) yazacağım bundan sonra.
Peki yukardaki ifadenin içinde ayrıca A(x_m)^2 + B(x_m) + C yani f(x_m) yok mu?
Dolayısıyla, 1 tane A(x_m+2)^2, 1 tane B(x_m+2), 1 tane A(x_m)^2, 1 tane B(x_m) ve 2 tane C kullanmış olduk. İfadeyi yeniden düzenleyelim:
Burada A’yı tekrar gruba alabiliriz:
Peki aşağıdaki ifade yerine
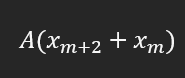
Şunu yazamaz mıyız?
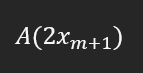
O halde, x_m+2 + x_m gördüğüm her yere 2x_(m+1) yazıyorum:
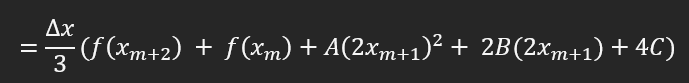
İfadeyi tekrar düzenliyorum:
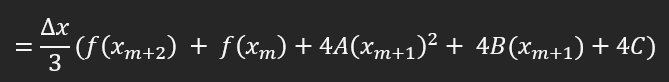
Son ifadenin içinde f(x_m+1)'ye ait bileşeler var. Tekrar sadeleştiriyorum:
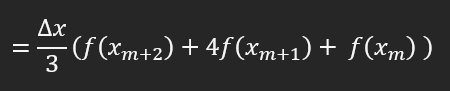
Evet, gördüğünüz gibi kullandığım formülü elde ettik. Bu formülün, işlem sayısı daha az olduğu için sizin paylaştığınız formülden daha hızlı hesaplama yapması gerekiyor.
Kolay gelsin.
5 Beğeni
4 sene sonrasindan suna bakiyorum da, ne kadar guzel bir etkilesim olmus. Duzgun soru, cevaplar, tartismalar, cevaplara cevaplar… Bugun olsa ikinizi ovmekten cevap yazmaya vaktim kalmazdi herhalde.
3 Beğeni
Bugün, dört sene öncesine bakarak diyebilirim ki, dört sene önce soruya yukardaki gibi bir cevap verebilecek durumda değilmişim. Böyle bir cevabı ancak konu hakkında okumalar yaptıktan sonra verebiliyorum. Geç kaldım biraz, katılıyorum, onun için eleştiriyorum kendimi. Ama bir yandan, iyi ki de okumuşum. 
Bu arada, daha önce göremediğim bazı ayrıntıları fark etmemi sağlayan, oldukça orijinal bulduğum bir zihnin var. Senin gibi yazılarını merakla okuduğum birkaç arkadaş daha var. İyi ki varsınız. Sizlerle güzel burası.
1 Beğeni
Bir kişi de dememiş ki, arkadaş sen onubunu bırak da threading kullan.
Peki, threading ile bir örnek yapalım ve sonuçları karşılaştıralım. threading’i aşağıdaki gibi uyguluyorum:
import timeit
from threading import Thread
def simpsons_original(f, n: int, a: int, b: int):
return sum(f(a + (i * d)) + 4 * f(a + ((i + 1) * d)) + f(a + ((i + 2) * d)) for i in range(0, n, 2)) * d / 3 if (d := (b - a) / n) else 0
def simpsons_copy(f, d: float, start: int, end: int, a: int, results: list):
results.append(sum(f(a + (i * d)) + 4 * f(a + ((i + 1) * d)) + f(a + ((i + 2) * d)) for i in range(start, end, 2)) * d / 3)
def simpsons_with_threads(f, n: int, a: int, b: int, n_threads: int):
results = []
threads = []
chunk_size = n // n_threads
d = (b - a) / n
for i in range(n_threads):
start = i * chunk_size
end = start + chunk_size
thread = Thread(target=lambda: simpsons_copy(f, d, start, end, a, results))
threads.append(thread)
thread.start()
for thread in threads:
thread.join()
return sum(results)
for i in range(1, 17):
t1 = timeit.timeit(stmt=lambda: simpsons_original(f=lambda x: x ** 2, n=10**6, a=0, b=10), number=1)
t2 = timeit.timeit(stmt=lambda: simpsons_with_threads(f=lambda x: x ** 2, n=10**6, a=0, b=10, n_threads=i), number=1)
ratio = t1 / t2
if t1 > t2:
msg = f"Runs faster with {i}-threads. ratio: {ratio}"
else:
msg = f"Runs slower with {i}-threads. ratio: {ratio}"
print(msg)
simpsons_original ile simpsons_with_threads fonksiyonlarına aynı argümanları veriyoruz ve değişik n_threads değerleri ile fonksiyonları karşılaştırıyoruz. Aldığım sonuçlar şöyle:
Runs slower with 1-threads. ratio: 0.9979086333410795
Runs slower with 2-threads. ratio: 0.9743791555620147
Runs slower with 3-threads. ratio: 0.9804025299131656
Runs slower with 4-threads. ratio: 0.9922557726659754
Runs slower with 5-threads. ratio: 0.9739442181000324
Runs slower with 6-threads. ratio: 0.9671743470262765
Runs slower with 7-threads. ratio: 0.9654450372027157
Runs slower with 8-threads. ratio: 0.9699793514100459
Runs slower with 9-threads. ratio: 0.9668114703027608
Runs slower with 10-threads. ratio: 0.970934392333783
Runs slower with 11-threads. ratio: 0.9815672867920567
Runs slower with 12-threads. ratio: 0.9667192092058771
Runs slower with 13-threads. ratio: 0.9696199309585157
Runs slower with 14-threads. ratio: 0.9598510768426152
Runs slower with 15-threads. ratio: 0.9604715933221863
Runs slower with 16-threads. ratio: 0.9504975415207115
Sonuçlara bakılırsa, threading kullanmak fonksiyonun daha yavaş çalışmasını sağlamış. Hatta, en iyi performansı, tek bir Thread kullandığımızda almışız, Thread sayısı artıkça da performans azalma eğilimi göstermiş.
Bu deneyi bir kaç kez tekrarlayınca, şöyle bir sonuçla karşılaşıyoruz:
n_threads ne kadar azsa, performans o kadar orijinal fonksiyonun performansında oluyor. n_threads artıkça, performans da düşmeye başlıyor. n_threads=1 durumunda, tesadüfen threading kullandığımız fonksiyon hızlı çalışabilir. Fakat aynı deneyi tekrar edince de tesadüfen orijinal fonksiyonumuz daha hızlı çalışabilir.
Bu sonuçlar doğrultusunda, tek bir thread kullanmanın da fonksiyonu daha hızlı çalıştıracağının bir garantisi yok. Bu tıpkı bir fonksiyonun çalışma zamanını iki kez üst üste ölçüp, iki sürenin de birbirine eşit olmamasına benziyor.
O halde threading kullanmak, bu tür sıralı CPU hesaplama işlemlerini yürüten fonksiyonları hızlandırmak yerine tam tersi bir etkiye neden oluyor. threading’e duyulan ihtiyacın, işlemleri hızlandırmak ile ilgisi yok aslında. Threading, genelde, beklemeye yol açacak türden işlemlerin, birbirlerini beklemeden, yani boşta durmadan çalışabilmeleri için kullanılıyor. Yukardaki kodların gerçekleştirdiği işlemler, birinin diğerinin gerçekleşmesini engelleyecek veya bir kaç işlemin beklemesine yol açacak türden işlemler olmadıkları için threading kullanmak faydadan çok zarar veriyor.
Aşağıdaki bağlantılara da bir göz atın isterseniz.
Threading is about taking advantage of idle resources to handle more work. If you have no idle resources, multi-threading has no advantages, so the overhead would actually make your overall runtime longer.
Merhaba,
Bu mesajda farklı integral teknikleri hakkında biraz bilgi paylaşayım istiyorum. Basit veya karmaşık bir çok farklı integral alma yöntemi var. Bu yöntemlerin daha basit olanlarından bahsetmek istiyorum. Daha karmaşık olanlarından bahsetmeyeceğim çünkü henüz anlamış değilim. 
Bahsedeceğim yöntemlerin ayrıca adaptif (uyarlanabilir) versiyonlarının algoritmalarını da paylaşacağım.
İlk olarak Monte Carlo entegrasyon yöntemiyle başlayabiliriz. Monte Carlo yönteminin genel algoritması şöyle özetlenebilir:
from math import pi
from random import uniform
def monte_carlo_integration(f, a, b, n):
return (b - a) / n * sum(f(uniform(a, b)) for _ in range(n))
Bu yöntemle pi sayısını kestirmeye çalışalım. Pi sayısının hesaplanmasıyla alakalı şöyle bir başlık da açılmış bu arada:
a = 0
b = 1
n = pow(10, 6)
f = lambda x: pow(1 - pow(x, 2), .5)
print(4 * monte_carlo_integration(f, a, b, n))
print(pi)
Çıktı:
3.14273191750064
3.141592653589793
Yukarda oluşturduğumuz monte carlo yönteminde, integralin hassasiyeti, üreteceğimiz nokta sayısına bağlıdır. Monte Carlo’nun adaptif versiyonunda ise integralin hassasiyeti, üretilecek nokta sayısına değil, bölümlere ayrılmış integrallere bağlıdır. Yukardaki monte carlo yöntemini, şöyle adaptif hale getirebiliriz:
from random import uniform
def adaptive_monte_carlo_integration(f, a, b, t):
def recursive_monte_carlo(f, a, b, t):
c = (a + b) / 2
left = (c - a) * f(uniform(a, c))
right = (b - c) * f(uniform(c, b))
area = left + right
if abs(area - (b - a) * f(uniform(a, b))) <= t:
return area
else:
return recursive_monte_carlo(f, a, c, t) + recursive_monte_carlo(f, c, b, t)
return recursive_monte_carlo(f, a, b, t)
Adaptif yöntemlerde, n parametresi yerine (0, 1) arasında olan ve tolerance anlamına gelen t parametresini kullanıyoruz. Adaptif Monte Carlo yöntemiyle pi sayısını kestirmeye çalışalım:
a = 0
b = 1
t = 1e-6
f = lambda x: pow(1 - pow(x, 2), .5)
print(4 * adaptive_monte_carlo_integration(f, a, b, t))
print(pi)
Çıktı:
3.1415897817240817
3.141592653589793
Adaptasyonu iki alana göre yapmak zorunda değiliz elbette. Üç alana göre de yapabilirsiniz.
def adaptive_monte_carlo__integration_v2(f, a, b, t):
def recursive_monte_carlo(f, a, b, t):
c = (2 * a + b) / 3
d = (2 * b + a) / 3
left = (c - a) * f(uniform(a, c))
mid = (d - c) * f(uniform(c, d))
right = (b - d) * f(uniform(d, b))
area = left + mid + right
if abs(area - (b - a) * f(uniform(a, b))) <= t:
return area
else:
return recursive_monte_carlo(f, a, c, t) + recursive_monte_carlo(f, c, d, t) + recursive_monte_carlo(f, d, b, t)
return recursive_monte_carlo(f, a, b, t)
İkinci Adaptif Monte Carlo yöntemiyle pi sayısını kestirmeye çalışalım:
a = 0
b = 1
t = 1e-6
f = lambda x: pow(1 - pow(x, 2), .5)
print(4 * adaptive_monte_carlo_integration_v2(f, a, b, t))
print(pi)
Çıktı:
3.141592560560807
3.141592653589793
Başka bir entegrasyon yöntemini ele alalım. Örneğin, 0. dereceden polinom (diktörtgen) kullanarak, Riemann entegrasyonu uygulayabiliriz. Metodun algoritması şu şekildedir:
def riemann_integration(f, a, b, n):
return (h := (b - a) / n) * sum(f(a + i * h) for i in range(n))
Riemann yöntemiyle pi sayısını kestirmeye çalışalım:
a = 0
b = 1
n = pow(10, 6)
f = lambda x: pow(1 - pow(x, 2), .5)
print(4 * riemann_integration(f, a, b, n))
print(pi)
Çıktı:
3.141594652413976
3.141592653589793
Şimdi de, Riemann’ın yöntemini adaptif hale getirelim:
def adaptive_riemann_integration(f, a, b, t):
def recursive_riemann(f, a, b, fa, fb, t):
c = (a + b) / 2
fc = f(c)
left = (c - a) * fa
right = (b - c) * fb
area = left + right
if abs(area - (b - a) * (fa + fb)) <= t:
return area
else:
return recursive_riemann(f, a, c, fa, fc, t) + recursive_riemann(f, c, b, fc, fb, t)
return recursive_riemann(f, a, b, f(a), f(b), t)
Adaptif Riemann yöntemiyle pi sayısını kestirmeye çalışalım:
a = 0
b = 1
t = 1e-6
f = lambda x: pow(1 - pow(x, 2), .5)
print(4 * adaptive_riemann_integration(f, a, b, t))
print(pi)
Çıktı:
3.141592480560611
3.141592653589793
Birinci dereceden polinom kullanarak da entegrasyon yapabiliriz. Birinci dereceden polinom kullanabileceğimiz yöntemlerden birisi Trapezoid’tir. Onun da algoritması şu şekilde:
def trapezoid_integration(f, a, b, n):
return 1 / 2 * (h := (b - a) / n) * sum(
sum(j * f(a + (i + k) * h) for k, j in enumerate([1, 1])) for i in range(n)
)
Trapezoid yöntemiyle pi sayısını kestirmeye çalışalım:
a = 0
b = 1
n = pow(10, 6)
f = lambda x: pow(1 - pow(x, 2), .5)
print(4 * trapezoid_integration(f, a, b, n))
print(pi)
Çıktı:
3.141592652413872
3.141592653589793
Pi sayısına daha fazla yaklaşmışız. Şimdi de adaptif bir trapezoid yöntemi oluşturalım:
def adaptive_trapezoid_integration(f, a, b, t):
def recursive_trapezoid(f, a, b, fa, fb, t):
c = (a + b) / 2
fc = f(c)
left = 1/2 * (c - a) * (fa + fc)
right = 1/2 * (b - c) * (fc + fb)
area = left + right
if abs(area - 1/2 * (b - a) * (fa + fb)) < t:
return area
else:
return recursive_trapezoid(f, a, c, fa, fc, t) + recursive_trapezoid(f, c, b, fc, fb, t)
return recursive_trapezoid(f, a, b, f(a), f(b), t)
Adaptif Trapezoid integrasyon yöntemiyle pi sayısını kestirmeye çalışalım:
a = 0
b = 1
t = 1e-20
f = lambda x: pow(1 - pow(x, 2), .5)
print(4 * adaptive_trapezoid_integration(f, a, b, t))
print(pi)
3.1415926535897705
3.141592653589793
Pi’ye daha da yaklaşmışız.
Polinom derecesinin 2 olduğu durumda Milne kuralını uygulayabiliriz. Onun algoritması ise şöyle:
def milnes_rule_integration(f, a, b, n):
return 4 / 3 * (h := (b - a) / n) * sum(
sum(j * f(a + (i + k / 4) * h) for k, j in enumerate([2, -1, 2])) for i in range(0, n, 4)
)
Milne kuralıyla pi sayısını kestirmeye çalışalım:
a = 0
b = 1
n = pow(10, 6)
f = lambda x: pow(1 - pow(x, 2), .5)
print(4 * milnes_rule_integration(f, a, b, n))
print(pi)
Çıktı:
3.141599646107457
3.141592653589793
Milne’nin yöntemini adaptif hale getirelim:
def adaptive_milnes_rule_integration(f, a, b, t):
def recursive_miles_rule(f, a, b, fa, fb, t):
c = (a + b) / 2
fc = f(c)
d = (a + c) / 2
e = (c + b) / 2
fd = f(d)
fe = f(e)
left = 4/3 * (c - a) / 4 * (2 * fa + -1 * fd + 2 * fc)
right = 4/3 * (b - c) / 4 * (2 * fc + -1 * fe + 2 * fb)
area = left + right
if abs(area - 4/3 * (b - a) / 4 * (2 * fa + -1 * fc + 2 * fb)) <= t:
return area
else:
return recursive_miles_rule(f, a, c, fa, fc, t) + recursive_miles_rule(f, c, b, fc, fb, t)
return recursive_miles_rule(f, a, b, f(a), f(b), t)
Adaptif Milne kuralı integrasyon yöntemiyle pi sayısını kestirmeye çalışalım:
a = 0
b = 1
t = 1e-20
f = lambda x: pow(1 - pow(x, 2), .5)
print(4 * adaptive_milnes_rule_integration(f, a, b, t))
print(pi)
3.1415926535897736
3.141592653589793
Bu yöntemle de pi’ye baya yaklaşmışız.
İkinci dereceden polinom kullanabileceğimiz başka bir entegrasyon yöntemi ise Simpson 1/3 kuralı. Onun algoritması da şöyle:
def simpson_1_3_integration(f, a, b, n):
return 1 / 3 * (h := (b - a) / n) * sum(
sum(j * f(a + (i + k) * h) for k, j in enumerate([1, 4, 1])) for i in range(0, n, 2)
)
Simpson 1/3 yöntemiyle pi sayısını kestirmeye çalışalım:
a = 0
b = 1
n = pow(10, 6)
f = lambda x: pow(1 - pow(x, 2), .5)
print(4 * simpson_1_3_integration(f, a, b, n))
print(pi)
Çıktı:
3.1415926531305414
3.141592653589793
Simpson 1/3 kuralını adaptif hale getirelim:
def adaptive_simpson_1_3_integration(f, a, b, t):
def recursive_simpson_1_3(f, a, b, fa, fb, t):
c = (a + b) / 2
fc = f(c)
d = (a + c) / 2
e = (c + b) / 2
fd = f(d)
fe = f(e)
left = 1/3 * (c - a) / 2 * (fa + 4 * fd + fc)
right = 1/3 * (b - c) / 2 * (fc + 4 * fe + fb)
area = left + right
if abs(area - 1/3 * (b - a) / 2 * (fa + 4 * fc + fb)) <= t:
return area
else:
return recursive_simpson_1_3(f, a, c, fa, fc, t) + recursive_simpson_1_3(f, c, b, fc, fb, t)
return recursive_simpson_1_3(f, a, b, f(a), f(b), t)
Adaptif Simpson 1/3 integrasyon yöntemiyle pi sayısını kestirmeye çalışalım:
a = 0
b = 1
t = 1e-20
f = lambda x: pow(1 - pow(x, 2), .5)
print(4 * adaptive_simpson_1_3_integration(f, a, b, t))
print(pi)
Çıktı:
3.141592653589793
3.141592653589793
Polinomun derecesini 3’e çıkardığımızda, Simpson 3/8 kuralıyla entegrasyon yapabiliriz. Onun algoritması da şöyle:
def simpson_3_8_integration(f, a, b, n):
return 3 / 8 * (h := (b - a) / n) * sum(
sum(j * f(a + (i + k / 3) * h) for k, j in enumerate([1, 3, 3, 1])) for i in range(0, n, 3)
)
Simpson 3/8 yöntemiyle pi sayısını kestirmeye çalışalım:
a = 0
b = 1
n = pow(10, 6)
f = lambda x: pow(1 - pow(x, 2), .5)
print(4 * simpson_3_8_integration(f, a, b, n))
print(pi)
Çıktı:
3.141596654558362
3.141592653589793
Simpson 3/8 yöntemini adaptif hale getirelim:
def adaptive_simpson_3_8_integration(f, a, b, t):
def recursive_simpson_3_8(f, a, b, fa, fb, t):
c = (a + b) / 2
d = (2 * a + c) / 3
e = (2 * c + a) / 3
o = (2 * c + b) / 3
m = (2 * b + c) / 3
fc = f(c)
fd = f(d)
fe = f(e)
fo = f(o)
fm = f(m)
left = 3/8 * (c - a) / 3 * (fa + 3 * fd + 3 * fe + fc)
right = 3/8 * (b - c) / 3 * (fc + 3 * fo + 3 * fm + fb)
area = left + right
if abs(area - 3/8 * (b - a) / 3 * (fa + 3 * fe + 3 * fo + fb)) <= t:
return area
else:
return recursive_simpson_3_8(f, a, c, fa, fc, t) + recursive_simpson_3_8(f, c, b, fc, fb, t)
return recursive_simpson_3_8(f, a, b, f(a), f(b), t)
Adaptif Simpson 3/8 integrasyon yöntemiyle pi sayısını kestirmeye çalışalım:
a = 0
b = 1
t = 1e-20
f = lambda x: pow(1 - pow(x, 2), .5)
print(4 * adaptive_simpson_3_8_integration(f, a, b, n))
print(pi)
Çıktı:
3.141592653589793
3.141592653589793
Bu da, iyi bir sonuç verdi.
Polinomun derecesini 4’e çıkartalım. 4. dereceden polinom kullanabileceğimiz entegrasyon yöntemi Boole’nin yöntemidir ve algoritması aşağıdaki gibidir:
def booles_rule_integration(f, a, b, n):
return 1 / 90 * (h := (b - a) / n) * sum(
sum(j * f(a + (i + k / 4) * h) for k, j in enumerate([7, 32, 12, 32, 7])) for i in range(n)
)
a = 0
b = 1
n = pow(10, 6)
f = lambda x: pow(1 - pow(x, 2), .5)
print(4 * booles_rule_integration(f, a, b, n))
print(pi)
Çıktı:
3.141592653539437
3.141592653589793
Şimdi de, Boole kuralını adaptif hale getirelim:
def adaptive_booles_rule_integration(f, a, b, t):
def recursive_booles_rule(f, a, b, fa, fb, t):
c = (a + b) / 2
d = (3 * a + c) / 4
e = (a + c) / 2
g = (3 * c + a) / 4
h = (3 * c + b) / 4
m = (c + b) / 2
o = (3 * b + c) / 4
fc = f(c)
fd = f(d)
fe = f(e)
fg = f(g)
fh = f(h)
fm = f(m)
fo = f(o)
left = 1/90 * (c - a) * (7 * fa + 32 * fd + 12 * fe + 32 * fg + 7 * fc)
right = 1/90 * (b - c) * (7 * fc + 32 * fh + 12 * fm + 32 * fo + 7 * fb)
area = left + right
if abs(area - 1/90 * (b - a) * (7 * fa + 32 * fe + 12 * fc + 32 * fm + 7 * fb)) <= t:
return area
else:
return recursive_booles_rule(f, a, c, fa, fc, t) + recursive_booles_rule(f, c, b, fc, fb, t)
return recursive_booles_rule(f, a, b, f(a), f(b), t)
Adaptif Boole integrasyon yöntemiyle pi sayısını kestirmeye çalışalım:
a = 0
b = 1
t = 1e-20
f = lambda x: pow(1 - pow(x, 2), .5)
print(4 * adaptive_booles_rule_integration(f, a, b, t))
print(pi)
Çıktı:
3.141592653589793
3.141592653589793
Daha başka entegrasyon yöntemleri de var elbette. Başta da dediğim gibi, bu algoritmalar daha karmaşık yapıdalar. Alan içerisine yerleştirilecek şeklin kaçıncı dereceden bir polinom olacağına bağlı olarak yöntem icat etmek mümkün. 1. dereceden bir polinomun katsayıları [1, 1], iken 2. dereceden bir polinomun katsayıları [1, 4, 1], 3. dereceden bir polinomun katsayıları [1, 3, 3, 1], 4. dereceden bir polinomun katsayıları ise [7, 32, 12, 32, 7] olur. Bu katsayılara Newton-Cotes katsayıları da deniyor.
Şimdilik paylaşacaklarımın sonuna geldik. Faydası olur diye umuyorum. Tekrar görüşmek üzere. Sağlıcakla kalın.
4 Beğeni
Yalnız iyi saçmalamışım.
Bozmamak için şöyle bir soru soruyum, Taylor kullanmak da etkili bir yöntem olmaz mı?
Dediğim gibi bir çok yöntem var. Algoritmasını öğrenmediğim veya henüz anlamadığım yöntemlerden bahsetmiyorum. Siz biliyorsanız paylaşın lütfen, incelemekten büyük keyif alırım.
Tekrar merhaba,
Konuyla alakalı olarak en azından bir önceki mesajıma göre daha açıklayıcı bir cevap vermiş olayım:
Taylor serileri analitik fonksiyonların yaklaşık değerlerini kestirmek için kullanılıyor. Bir f(x) fonksiyonu, tanım kümesindeki her bir x değeri için türevlenebilir ise o fonksiyon analitiktir. Ancak f(x) fonksiyonunun tanım kümesinde yer alan her bir x noktası için sonsuz kere türevlenebilir olup olmaması önemli değil. Önemli olan f(x)'in tanım kümesindeki her nokta için türevlenebilir olması.
Taylor serileri doğrudan integral alma işlemi için kullanılmıyor. Yukarda da bahsettiğim gibi analitik fonksiyonları kestirmek için kullanılıyor.
Mesela üstel artış serisi, Taylor Serisine uyar. e’yi kestirmek için Taylor Serileri kullanılabilir.
from math import factorial
def exponential(n: int, x: int):
return sum(pow(x, i) / factorial(i) for i in range(n))
Burada x = 1 için n terim sayısını değiştirerek aldığımız sonuca bakabiliriz:
for i in range(20):
print(exponential(n=i, x=1))
Sonuç:
0
1.0
2.0
2.5
2.6666666666666665
2.708333333333333
2.7166666666666663
2.7180555555555554
2.7182539682539684
2.71827876984127
2.7182815255731922
2.7182818011463845
2.718281826198493
2.7182818282861687
2.7182818284467594
2.71828182845823
2.718281828458995
2.718281828459043
2.7182818284590455
2.7182818284590455
Gördüğünüz gibi x = 1 için polinomun derecesini artırdıkça e sayısına yaklaşıyoruz:
from math import exp, e
print(e)
print(exp(1))
Çıktı:
2.718281828459045
2.718281828459045
Taylor Serilerini ayrıca doğal logaritma hesaplarken kullanabiliriz:
from math import log
def ln(n: int, x: float):
return sum(pow(-1, i - 1) * pow(x - 1, i) / i for i in range(1, n))
print(log(1.5))
print(ln(n=11, x=1.5))
Çıktı:
0.4054651081081644
0.4054346478174603
Yukardaki fonksiyon ile, |x - 1| <= 1 & x != 0 için kestirimler yapabiliriz. Başka x değerleri için logaritma fonksiyonunda değişiklikler yapmak gerekiyor.
Taylor serilerini, cosinus fonksiyonunun sonucunu kestirmek için de kullanabiliriz. Mesela 9. dereceden bir polinom ile cosinus fonksiyonu ile bir değer üretelim:
from math import cos, radians, factorial
def cosinus(n: int, x: float):
return sum(pow(-1, i) * pow(x, 2 * i) / factorial(2 * i) for i in range(n))
print(cos(radians(45)))
print(cosinus(n=9, x=radians(45)))
Sonuç:
0.7071067811865476
0.7071067811865475
Veya sinüs fonksiyonunu simüle edebilirsiniz:
from math import sin, radians, factorial
def sinus(n: int, x: float):
return sum(pow(-1, i) * pow(x, 2 * i + 1) / factorial(2 * i + 1) for i in range(n))
print(sin(radians(30)))
print(sinus(n=9, x=radians(30)))
Çıktı:
0.49999999999999994
0.49999999999999994
Mesela tanjant fonksiyonunu simüle edebiliriz. Tanjantı hesaplamak için Bernoulli serisini de kullanmak gerekiyor.
from math import comb
def nth_bernoulli(n):
b = [0.0] * (n + 1)
for m in range(n + 1):
for k in range(m + 1):
for v in range(k + 1):
b[m] += pow(-1, v) * comb(k, v) * pow(v, m) / (k + 1)
return b
Şimdi tanjant fonksiyonunu yazabiliriz:
from math import factorial, radians, tan
def tangent(n: int, x: float):
return sum(nth_bernoulli(2 * i)[2 * i] * pow(-4, i) * (1 - pow(4, i)) * pow(x, 2 * i - 1) / factorial(2 * i) for i in range(n))
print(tangent(n=9, x=radians(30)))
print(tan(radians(30)))
Sonuç:
0.5773536596927821
0.5773502691896257
Özetlemek gerekirse; trigonometrik ve hiperbolik fonksiyonların sonuçlarının kestirilmesinde, doğal logaritma hesaplamalarında, üstel fonksiyonların hesaplamalarında, binom serisi hesaplamalarında, geometrik serilerin açılımlarında Taylor Serileri veya diğer bir ifadeyle Maclaurin serileri kullanılıyor.
Şimdilik paylaşacaklarım bunlar. Tekrar görüşmek üzere.
1 Beğeni
Mesela çok da anlamadığım, algoritmalarını oldukça karışık bulduğum yöntemlerden olan Gauss-Kronrod, Gauss-Chebyshev, Gauss-Legendre gibi entegrasyon yöntemlerinde cos fonksiyonu kullanılıyor. cos fonksiyonunu, Taylor Serilerini kullanarak oluşturabileceğimizi gördük. O halde, doğrudan integral hesaplamak için olmasa da, bir integral yönteminin formülünde yer alan cos gibi bir analitik fonksiyonun yaklaşık değerini hesaplamak için Taylor Serileri kullanılır.
1 Beğeni
Çok güzel.
Bu arada, özel olarak bir şeyi belirtmek isterim sevgili @dildeolupbiten , ben “Taylor Serileri veya diğer bir ifadeyle Maclaurin serileri” ifadesini kabul etmiyorum.
Neticede genelleştirdiği için Taylor’un bir hakkı var. İnsanlar, genel olarak formülleri genelleştirenleri çok önemsemezler bilim tarihinde.
Çünkü genelleştirmek, gözlem, hesaplamalar sonucundaki ilk özel bulguların(yani ilgili disiplinin kendi alanındaki ilk geçerli olmuş hipotezlerinin) yarattığı sansasyonel etkinin yanında, tarihi süreçte “basit bir şey” gibi gelir insanlara. Halbuki genelleştirmek ve sadeleştirmek bilimin esas amacıdır.
Mesela bu haksızlığın aynısı Louis de Broglie için de yapılmıştır.
Einstein ve Planck’ın formüllerinden daha genel bir formüle ulaştığı için, bunu çok kıymetli görmediler onun zamanında da.
Bana göre, asıl kıymetli olanlar, “genel formülleri” tespit edenlerdir.
Bunu da belirtmek isterim.
Sevgiler.