PI sabiti hesaplama algoritması

Python
1

Eskilere denk geldikçe paylaşıyorum. Algoritmaya wikipedia’dan bakmıştım da kapalı şimdi bulamadım.

#-*- coding: utf-8 -*-

# Author:    Fatih Mert Doğancan
# Date:      02.12.2014

def arccot(x, u):
    sum = ussu = u // x
    n = 3
    sign = -1
    while 1:
        ussu = ussu // (x*x)
        term = ussu // n
        if not term:
            break
        sum += sign * term
        sign = -sign
        n += 2
    return sum

def pi(basamak):
    u = 10**(basamak+10)
    pi = 4 * (4*arccot(5,u) - arccot(239,u))
    return pi // 10**10

if __name__ == "__main__":
    print pi(1000) # 1000 basamaklı bi sayısı
2

Pi sayısını hesaplamak için Monte Carlo tümlev alma yöntemi de kullanılabilir.

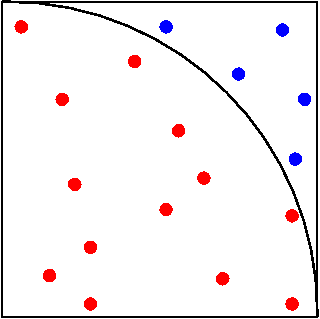
Birim çemberin alanının pi olduğunu ve çeyreğinin alanının da pi/4 olduğunu bildiğimiz için çeyrek çemberi kullanıyoruz.

Burada rastgele noktalar koyuyoruz. Daha sonra çemberin içine düşen noktalarla toplam noktaların oranını buluyoruz. Örneğin 10 nokta koymuşsak ve bunlardan 9 tanesi çemberin içine düştüyse

çemberin içine düşen nokta / toplam nokta = 0.9

olmuş oluyor.

Peki noktanın çemberin içinde olduğunu nasıl anlıyoruz.

(x,y) noktamız olsun. Çemberin denklemi x^2 + y^2 idi hatırlayacağınız üzere. Yarıçapı 1 olan çember kullandığımız için x^2+y^2 <= 1 ise nokta çemberin içinde değilse dışında oluyor.

Bu şekilde örneğin 1.000.000 kadar nokta oluşturduğumuzda çemberin içine dışına düşen noktaların oranı 0.786054 gibi bir rakam çıkıyor. Bunu dörtle çarptığımızda

pi = 4 * 0.786054 = 3.144216 gibi bir rakam çıkıyor.

Bahsettiğim gibi Monte Carlo bir tümlev alma yöntemi olduğu için tümlevi alınabilen tüm işlevlerle kullanabiliyoruz. Diğer yöntemlerle kolayca tümlevi alınamayan, ya da hesaplanması güç katlı tümlev hesabında Monte Carlo integrali kullanılıyor.

Merak edenler için Python programını da yazayım.

import math
import random
 
# from time import perf_counter
# burayı alttaki satırla değiştirdim
 
from timeit import default_timer as perf_counter
 
def monte_carlo(start, stop, num_points, f):
    hits = 0
    upp_bound = 0
    for i in range(num_points):
        x = random.uniform(start, stop)
        y = random.uniform(0, 4) # this is cheating since I already know it's 4
        if y <= f(x):
            hits += 1
        if y > upp_bound:
            upp_bound = y
    ans = (hits / num_points) * ((stop - start) * upp_bound)
    return ans
 
def riemann(start, stop, step, f):
    return sum(f(start+step*m)*step for m in range(int((stop - start)/step)))
 
f = lambda x: math.sqrt(16 - 16*x**2)
 
start = perf_counter()
a = monte_carlo(0, 1, 10000000, f)
m_time = perf_counter() - start
start = perf_counter()
b = riemann(0, 1, 1/15000, f)
r_time = perf_counter() - start
print('Monte Carlo: %s\nTime elapsed: %s' % (a, m_time))
print('Riemann sum: %s\nTime elapsed: %s' % (b, r_time))
2 Beğeni
3

Benim bu seviyeye gelebilmem için ne yapmam gerekiyor?

4

@Mehmet_Zerey Monte Carlo yöntemi hem bilgisayar bilimi, hem de yüksek matematiğin konuları arasına giriyor.

Pratikte uygulaması ise kolay sayılabilir.

Örnek olarak N x N boyutlarında bir ızgara oluşturuyoruz. Beyazlar açık, siyahlar kapalı noktaları, maviler ise suyu gösteriyor. Sonra alt ve üst arasında bir bağlantı sağlanıncaya kadar rastgele noktaları açıyoruz. Böylece beyazlardan oluşan yukarıdan aşağıya rastgele bir yol yapmış oluyoruz. Eğer su boşluklardan kendine bir yol bulabilirse alta doğru akıyor.

Bize Monte Carlo benzetim yöntemi kullanarak akış eşiğini, akış eşiğinin standart sapmasını hesaplamamızı istiyorlar. Pi sayısının hesabına benzer şekilde bu seferde açık kare sayısının toplam kare sayısına oranını buluyoruz. Örneğin 400 kare varsa ve 204 kare açıldığında akış gerçekleştiyse 204/400 akış eşiği 0.51 oluyor.

Bunun çalışan bir örneğinin görüntüsünü burada bulabilirsiniz.

Bu tür konuları öğrenmek için algoritma ve veri yapısı dersleri almak gerekebilir.

Bu dersi ve devamındaki dersi tavsiye edebilirim.

1 Beğeni
5

Teşekkürler zaman buldukça bakacağım bu konuya.

6

Yalnız bu kodların içerisinde ‘sum’ adlı değişkeni kullanmak iyi bir fikir değil. ‘sum’ gömülü bir fonksiyon ve kodların da Python 2x sürümleri için yazıldığını belirtmek, inceleyenler için kolaylık sağlar bana göre.