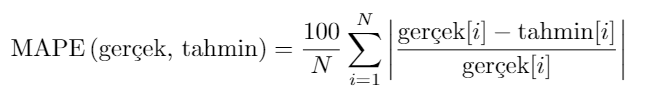MAE, MSE, RMSE, MAPE Hakkında

onurkizilarsan · Ağustos 16, 2021, 7:31ös

Arkadaşlar merhabalar,

Yapay Sinir Ağları ile yapmış olduğum çalışmamda takıldığım bir yer var. Sizlere danışmak istedim. Ben gerçek değerleri ve tahmin değerlerini sisteme tanıttım ve değerleri aldım. Aldığım sonuçlar da RMSE çok farklı çıktı acaba yapmış olduğum çalışma mı baştan hatalı yoksa RMSE mi hatalı anlayamadım. Aslında bunları birçok farklı siteden de teyit ettim hep bu şekilde kullanılmış ama bende sonuç çok farklı çıktı. Acaba nerede hata yapıyorum arkadaşlar. Bu konuda yardımlarınızı rica ediyorum.

Teşekkür ederim.

İlk önce kütüphaneleri yükledim.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from seaborn import heatmap
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.preprocessing import MinMaxScaler
from sklearn.neural_network import MLPRegressor
import matplotlib.style as mplstyle

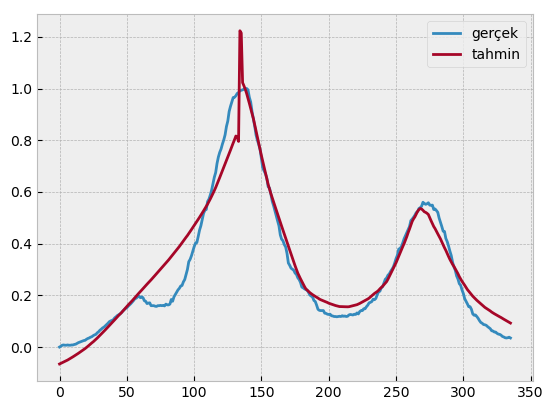
Gerçek değerleri sisteme yükledim.

gercek =[[0.   ],
       [0.003],
       [0.007],
       [0.008],
       [0.007],
       [0.007],
       [0.008],
       [0.007],
       [0.007],
       [0.008],
       [0.008],
       [0.01 ],
       [0.011],
       [0.014],
       [0.017],
       [0.019],
       [0.021],
       [0.023],
       [0.025],
       [0.026],
       [0.03 ],
       [0.033],
       [0.035],
       [0.038],
       [0.04 ],
       [0.044],
       [0.047],
       [0.049],
       [0.055],
       [0.059],
       [0.065],
       [0.069],
       [0.074],
       [0.077],
       [0.082],
       [0.087],
       [0.092],
       [0.098],
       [0.101],
       [0.103],
       [0.106],
       [0.113],
       [0.117],
       [0.122],
       [0.125],
       [0.128],
       [0.133],
       [0.139],
       [0.144],
       [0.149],
       [0.152],
       [0.158],
       [0.163],
       [0.168],
       [0.174],
       [0.18 ],
       [0.187],
       [0.189],
       [0.194],
       [0.197],
       [0.191],
       [0.194],
       [0.191],
       [0.179],
       [0.177],
       [0.168],
       [0.17 ],
       [0.171],
       [0.16 ],
       [0.16 ],
       [0.16 ],
       [0.158],
       [0.157],
       [0.16 ],
       [0.16 ],
       [0.161],
       [0.16 ],
       [0.161],
       [0.159],
       [0.166],
       [0.163],
       [0.163],
       [0.166],
       [0.184],
       [0.177],
       [0.194],
       [0.203],
       [0.212],
       [0.221],
       [0.227],
       [0.236],
       [0.238],
       [0.252],
       [0.261],
       [0.281],
       [0.3  ],
       [0.33 ],
       [0.339],
       [0.353],
       [0.371],
       [0.388],
       [0.402],
       [0.404],
       [0.427],
       [0.452],
       [0.469],
       [0.494],
       [0.517],
       [0.529],
       [0.532],
       [0.563],
       [0.572],
       [0.588],
       [0.607],
       [0.633],
       [0.657],
       [0.675],
       [0.71 ],
       [0.735],
       [0.753],
       [0.766],
       [0.785],
       [0.801],
       [0.821],
       [0.853],
       [0.874],
       [0.911],
       [0.931],
       [0.948],
       [0.965],
       [0.966],
       [0.972],
       [0.981],
       [0.984],
       [0.992],
       [0.993],
       [0.995],
       [0.997],
       [0.999],
       [1.   ],
       [0.995],
       [0.966],
       [0.948],
       [0.911],
       [0.882],
       [0.854],
       [0.82 ],
       [0.8  ],
       [0.783],
       [0.764],
       [0.727],
       [0.692],
       [0.681],
       [0.67 ],
       [0.653],
       [0.62 ],
       [0.615],
       [0.592],
       [0.564],
       [0.547],
       [0.527],
       [0.507],
       [0.488],
       [0.469],
       [0.434],
       [0.417],
       [0.411],
       [0.396],
       [0.387],
       [0.362],
       [0.325],
       [0.316],
       [0.305],
       [0.301],
       [0.297],
       [0.286],
       [0.281],
       [0.268],
       [0.261],
       [0.25 ],
       [0.232],
       [0.229],
       [0.225],
       [0.222],
       [0.22 ],
       [0.211],
       [0.201],
       [0.197],
       [0.193],
       [0.18 ],
       [0.176],
       [0.162],
       [0.146],
       [0.142],
       [0.141],
       [0.141],
       [0.141],
       [0.131],
       [0.13 ],
       [0.127],
       [0.126],
       [0.127],
       [0.121],
       [0.12 ],
       [0.118],
       [0.118],
       [0.117],
       [0.118],
       [0.119],
       [0.118],
       [0.121],
       [0.119],
       [0.12 ],
       [0.118],
       [0.119],
       [0.124],
       [0.126],
       [0.125],
       [0.124],
       [0.127],
       [0.126],
       [0.132],
       [0.128],
       [0.137],
       [0.141],
       [0.141],
       [0.148],
       [0.148],
       [0.156],
       [0.162],
       [0.171],
       [0.173],
       [0.176],
       [0.185],
       [0.183],
       [0.188],
       [0.202],
       [0.214],
       [0.216],
       [0.229],
       [0.233],
       [0.247],
       [0.262],
       [0.267],
       [0.278],
       [0.283],
       [0.293],
       [0.301],
       [0.31 ],
       [0.325],
       [0.342],
       [0.355],
       [0.379],
       [0.381],
       [0.389],
       [0.403],
       [0.419],
       [0.431],
       [0.442],
       [0.455],
       [0.466],
       [0.489],
       [0.495],
       [0.502],
       [0.51 ],
       [0.52 ],
       [0.524],
       [0.536],
       [0.539],
       [0.545],
       [0.56 ],
       [0.555],
       [0.552],
       [0.554],
       [0.558],
       [0.549],
       [0.548],
       [0.549],
       [0.532],
       [0.534],
       [0.528],
       [0.521],
       [0.499],
       [0.483],
       [0.466],
       [0.448],
       [0.447],
       [0.42 ],
       [0.408],
       [0.391],
       [0.371],
       [0.354],
       [0.328],
       [0.31 ],
       [0.297],
       [0.275],
       [0.263],
       [0.245],
       [0.239],
       [0.221],
       [0.207],
       [0.187],
       [0.177],
       [0.167],
       [0.156],
       [0.156],
       [0.146],
       [0.128],
       [0.123],
       [0.124],
       [0.118],
       [0.111],
       [0.102],
       [0.095],
       [0.092],
       [0.087],
       [0.086],
       [0.084],
       [0.079],
       [0.075],
       [0.071],
       [0.063],
       [0.062],
       [0.058],
       [0.058],
       [0.053],
       [0.05 ],
       [0.049],
       [0.046],
       [0.041],
       [0.039],
       [0.036],
       [0.035],
       [0.036],
       [0.038],
       [0.035]]

Tahmin değerlerini de yükledim.

tahmin = [-0.06556226, -0.0630848 , -0.06046269, -0.05787102, -0.05545763,
       -0.05299102, -0.05028735, -0.04722935, -0.04420993, -0.04107783,
       -0.03769426, -0.0343948 , -0.0310631 , -0.02774986, -0.02420329,
       -0.02061693, -0.01692122, -0.01331198, -0.00981569, -0.00594669,
       -0.00180908,  0.00256205,  0.00716172,  0.01161048,  0.01617378,
        0.02018835,  0.02492739,  0.02985189,  0.03466063,  0.03987593,
        0.04525816,  0.05046517,  0.0552874 ,  0.06087784,  0.06645482,
        0.07197837,  0.07766528,  0.08359708,  0.08898017,  0.09416841,
        0.09974325,  0.10555897,  0.11134482,  0.11691412,  0.12275013,
        0.12790063,  0.13305895,  0.13900764,  0.14493439,  0.15093538,
        0.15676003,  0.16268664,  0.16800253,  0.1731615 ,  0.17918687,
        0.18519632,  0.19123806,  0.19731139,  0.20331889,  0.2087972 ,
        0.21417818,  0.22001056,  0.22586121,  0.23154826,  0.23732293,
        0.24314263,  0.24855371,  0.25392929,  0.25984797,  0.26555804,
        0.27148635,  0.27747835,  0.28339264,  0.2892537 ,  0.29487956,
        0.30081387,  0.30677558,  0.31274173,  0.31882584,  0.325102  ,
        0.33111633,  0.33683914,  0.34327896,  0.34961833,  0.35605154,
        0.36255902,  0.36909622,  0.37544436,  0.38170371,  0.38887921,
        0.39588183,  0.40300029,  0.41029978,  0.41773217,  0.42460428,
        0.43135465,  0.43883729,  0.44664318,  0.45440732,  0.46219223,
        0.47007587,  0.47778464,  0.48562944,  0.49365491,  0.50169412,
        0.50984589,  0.5182253 ,  0.52685661,  0.53555597,  0.54405758,
        0.55300165,  0.56261088,  0.57272165,  0.58313284,  0.59411562,
        0.60524731,  0.61694626,  0.62950189,  0.6427228 ,  0.65563574,
        0.668758  ,  0.68179669,  0.69508431,  0.70797174,  0.72126312,
        0.73437084,  0.74810715,  0.76175877,  0.77604875,  0.78915883,
        0.80208213,  0.81616178,  0.8130123 ,  0.79532216,  1.22328373,
        1.21460527,  1.02266839,  1.0103224 ,  0.99685401,  0.98074448,
        0.96251967,  0.94309656,  0.92271483,  0.9031974 ,  0.8838064 ,
        0.8597168 ,  0.8364977 ,  0.81208507,  0.78772374,  0.76255595,
        0.73983384,  0.71726994,  0.69444887,  0.67238485,  0.65035152,
        0.62872289,  0.61051234,  0.59340796,  0.57706533,  0.56104037,
        0.54572264,  0.53045063,  0.51442273,  0.49836971,  0.48273092,
        0.46739901,  0.4518002 ,  0.43636628,  0.42091231,  0.40564425,
        0.39024272,  0.37508147,  0.3597239 ,  0.34437309,  0.32882145,
        0.31415571,  0.29993981,  0.28597156,  0.27457514,  0.26408038,
        0.25377635,  0.24363744,  0.23370204,  0.22488395,  0.2198244 ,
        0.21502065,  0.21022038,  0.20620895,  0.20246395,  0.19898014,
        0.19563155,  0.19247556,  0.18947496,  0.18565554,  0.18301828,
        0.18096968,  0.17910908,  0.17677994,  0.17438353,  0.17224781,
        0.16946478,  0.16763604,  0.16584564,  0.16394265,  0.16217391,
        0.16054142,  0.15924184,  0.15758819,  0.15655699,  0.15619595,
        0.15624924,  0.15621657,  0.15585002,  0.15568624,  0.15556212,
        0.15588946,  0.15726544,  0.15861634,  0.15968556,  0.16107156,
        0.16260747,  0.16384929,  0.16615797,  0.1686323 ,  0.17144247,
        0.17417941,  0.17719094,  0.18026209,  0.18239778,  0.18579083,
        0.18933117,  0.19387311,  0.19841941,  0.20315055,  0.20742898,
        0.21099678,  0.21458963,  0.21911244,  0.22508915,  0.22986735,
        0.23505815,  0.24087254,  0.24610402,  0.25305277,  0.26251367,
        0.27320176,  0.28334181,  0.29403893,  0.30571215,  0.3159626 ,
        0.32604152,  0.33870473,  0.35024564,  0.36337269,  0.37671687,
        0.38869628,  0.40029642,  0.41347161,  0.42732877,  0.44275253,
        0.45635845,  0.47128361,  0.48607357,  0.49578237,  0.50363189,
        0.51430386,  0.52469609,  0.53145515,  0.5358638 ,  0.53386717,
        0.52900245,  0.52329508,  0.52086879,  0.51731888,  0.51267858,
        0.50114032,  0.48875289,  0.47699399,  0.46620831,  0.45797318,
        0.44771781,  0.43786238,  0.4283838 ,  0.41832484,  0.40726706,
        0.3952404 ,  0.38396685,  0.37373213,  0.36169848,  0.3503001 ,
        0.33916133,  0.32952152,  0.31969423,  0.31186933,  0.30229311,
        0.29302864,  0.28348815,  0.27237391,  0.26288101,  0.25423315,
        0.24651994,  0.23894084,  0.23028006,  0.2223418 ,  0.21580854,
        0.20914175,  0.20295122,  0.19665488,  0.19139406,  0.18569776,
        0.18087774,  0.17625967,  0.17125058,  0.16645894,  0.16236113,
        0.15810729,  0.15335026,  0.14997967,  0.14631576,  0.14338665,
        0.13957659,  0.1353677 ,  0.13191954,  0.12884172,  0.12575756,
        0.12315787,  0.11975383,  0.11695596,  0.1142255 ,  0.1108604 ,
        0.10777419,  0.10474757,  0.10180082,  0.09876833,  0.09555455,
        0.09275043]

Ortalama Mutlak Hata (Mean Absolute Error) bulmaya tanıttım. Aldığım değer : MAE: 0.049466

from sklearn.metrics import mean_absolute_error
mae = mean_absolute_error(gercek, tahmin)
print('MAE: %f' % mae)

Ortalama Kare Hata (Mean Squared Error) bulmaya çalıştım. Aldığım değer : MSE: 0.004666

from sklearn.metrics import mean_squared_error
mse = mean_squared_error(gercek, tahmin)
print('MSE: %f' % mse)

Kök Ortalama Kare Hata (Root Mean Square Error) bulmaya çalıştım. Aldığım değer : RMSE: 0.068309

from sklearn.metrics import mean_squared_error
from math import sqrt
mse = mean_squared_error(gercek, tahmin)
rmse = sqrt(mse)
print('RMSE: %f' % rmse)

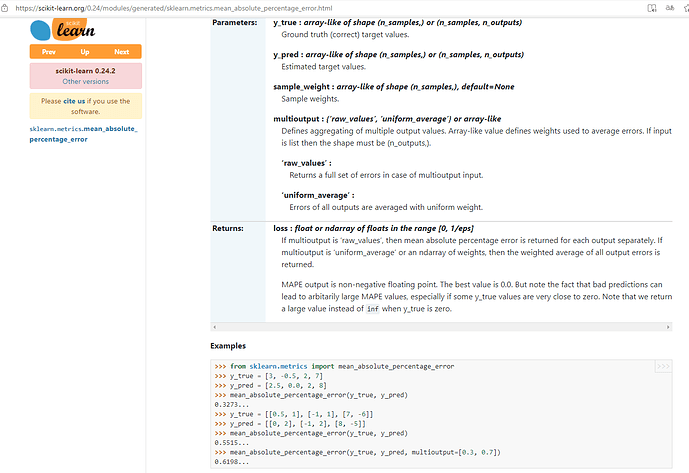
Ortalama Mutlak Yüzde Hata (Mean Absolute Percentage Error) bulmaya çalıştım. Aldığım değer : MAPE: 878768362219.564575

from sklearn.metrics import mean_absolute_percentage_error
mape = mean_absolute_percentage_error(gercek, tahmin)
print('MAPE: %f' % mape)

aib · Ağustos 16, 2021, 8:19ös

gercek ve tahmin'in ayni boyuta sahip olmalari gerekmiyor mu?

onurkizilarsan · Ağustos 16, 2021, 8:26ös

Aynı boyut derken gerçek ve tahmin değerleri ikisi de 336 adet sonuca sahipler. Bunu mu kastettiniz acaba ben mi yanlış anladım?

anon18277073 · Ağustos 16, 2021, 8:38ös

RMSE 0.068309 olarak normal duruyor aslında; daha az veya fazla bir değer mi bekliyordunuz (bu arada RMSE için squared=False paslayabilirsiniz mean_squared_error fonksiyonuna ama size kalmış).

onurkizilarsan · Ağustos 16, 2021, 8:55ös

Arkadaşlar çok çok özür dilerim. MAPE sonuçlarımdan şüphe ediyorum değer çok farklı çıktı bu konuda yazmıştım. Dalgınlık RMSE yazmışım. Tekrardan özür dilerim. MAPE olacak.

anon18277073 · Ağustos 16, 2021, 9:22ös

Estağfurullah ne özrü, MAPE’nin formülüne bakmış mıydınız? Bir bölme işlemi söz konusu.

onurkizilarsan · Ağustos 16, 2021, 9:27ös

Aslında ben Scikit-Learn sitesinden direk aldım. Orada her metrik değer için örnek vermiş. Ancak bende değerler neden böyle çıkıyor anlamadım. Bir çok farklı siteden de teyit ettim hepsinde de aynı kod bloğunu gördüm. İşin içinden çıkamadım doğrusu.

aib · Ağustos 16, 2021, 9:58ös

Evet ama biri (336, 1), digeri (336) gibi duruyor. Aralarinda cevrim yapmak kolay, fakat MAPE bunu yapiyor mu bilmiyorum.

Her halukarda list yerine data tipleri (dtype) ve boyutlari (shape) ayni olan numpy.ndarray’ler kullanmak iyi bir fikir.

onurkizilarsan · Ağustos 16, 2021, 10:01ös

Onu nasıl yapabilirim? Ben de yeni yeni öğreniyorum. Eğer dediğiniz çalışmayı kod olarak paylaşabilirseniz sevinirim. Çok teşekkürler.

aib · Ağustos 17, 2021, 8:17öö

gercek = numpy.array([[0.], [0.003], [0.007], ...], dtype=numpy.float32)
gercek_flat = gercek.reshape(-1)

https://numpy.org/doc/stable/reference/generated/numpy.ndarray.html
https://numpy.org/doc/stable/reference/routines.array-creation.html

anon18277073 · Ağustos 17, 2021, 9:05öö

Evet, ben aslında matematiksel formülünü sormuştum. Her ikisi de N uzunluğunda olan gerçek ve tahmin serileri arasında MAPE şöyle tanımlanıyor:

Gördüğünüz gibi hesabında bir bölme işlemi söz konusu. Bölme işlemi varsa sorun da çok uzak değildir zira bir sayıyı 0’a bölmek kim bilir neye eşit. Gelin görün ki sizin gercek listenizde de gerçekten 0 diye bir değer var; bu durumda MAPE sonsuz felan olabilirdi (ona da yakın sayılır).

Aslında bu “instability” sizin görselini attığınız sklearn dokümantasyonunda da belirtiliyor:

But note the fact that bad predictions can lead to arbitarily large MAPE values, especially if some y_true values are very close to zero. Note that we return a large value instead of inf when y_true is zero.

Son cümlede dedikleri ve kaynağından da gördüğümüz üzere

github.com

scikit-learn/scikit-learn/blob/2beed5584/sklearn/metrics/_regression.py#L261


      
          >>> y_pred = [[0, 2], [-1, 2], [8, -5]]
          >>> mean_absolute_percentage_error(y_true, y_pred)
          0.5515...
          >>> mean_absolute_percentage_error(y_true, y_pred, multioutput=[0.3, 0.7])
          0.6198...
          """
          y_type, y_true, y_pred, multioutput = _check_reg_targets(
              y_true, y_pred, multioutput)
          check_consistent_length(y_true, y_pred, sample_weight)
          epsilon = np.finfo(np.float64).eps
          mape = np.abs(y_pred - y_true) / np.maximum(np.abs(y_true), epsilon)
          output_errors = np.average(mape,
                                     weights=sample_weight, axis=0)
          if isinstance(multioutput, str):
              if multioutput == 'raw_values':
                  return output_errors
              elif multioutput == 'uniform_average':
                  # pass None as weights to np.average: uniform mean
                  multioutput = None
          
          return np.average(output_errors, weights=multioutput)

paydaya bir epsilon ekliyorlar (yaklaşık değeri 2.220446049250313e-16); dolayısıyla MAPE uçuyor gerçek değer sıfır (veya ona yakın) olduğunda.

Velhasıl, MAPE metriğinin, gerçek değerlerin 0 veya 0’a çok yakın olduğu durumlarda tercih edilmemesi daha iyi olur çünkü tanımı gereği böylesi durumlarda makul bir değer döndüremiyor. Oysaki tahminler ve gerçek değerler arasında uçurum yok. Bunu hem diğer metrikler hem de grafik söylüyor:

Bir diğer durum da hangi metriğin ne söylediği üzerine. Mesela MAPE’yi diğer üçünden (MAE, (R)MSE) ayıran bir özellik var: scale-independent olması. Tanımda gördüğümüz üzere gerçek ve tahmin değerlerinin birimleri neyse (örn. mili watt), bölme işlemi sayesinde birbirini götürüyorlar. Bu da birimden bağımsız bir metrik sağlıyor. Sizin bir modeliniz var diyelim, elinizde de 2 tane seri var tahmin edilmeye çalışılan. Ama birinin skalası 1000’ler düzeyinde diğerininki 10’lar düzeyinde. Eğer modelinizin performansını seriler arası karşılaştırmak istiyorsanız, ilk 3 metriği kullanmanız yanlış olur zira sırf değerlerin kendileri 1000’ler düzeyinde diye MAE ve (R)MSE değerleri yüksek çıkmaya yeltenecektir (örn. ilki için 1140, diğeri için 19 MAE geldi). Ama MAPE kullandığınıza, paydadaki elemanın bir nevi normalizasyon görevi görmesinden mütevellit elinizde karşılaştırılabilir iki sayı olacaktır (örn. ilki için 2.35%, diğeri için 2.99% MAPE) gelebilir.

Yine benzer şekilde skalaya bağlı ilk 3 metrik arasında da farklılıklar var. Örneğin MSE ve RMSE: ikinci ilkinin karekökünden ibaret; varoluş sebebi olarak elde edilen metriğin verinin birimiyle aynı olması ve bu sayede daha kolay yorumlanabilir olması söylenebilir. Örneğin kW’lık elektrik tüketimi tahmininde MSE 312 gelse (ki birimi kW kare olur), RMSE 17.66 kW geldi denilir. Yani model aşağı yukarı ortalama 17.66 kW hataya sahip diyebiliriz. Peki MSE ve MAE arasındaki fark? Formüllerine bakarsanız MSE hataların karelerini ortalarken, MAE mutlak değerlerini ortalıyor. Hemen iki sayıya bakalım: 10 ve 12 sırasıyla gerçek ve tahmini değerler olsun. MAE 2 verir, MSE 4. Peki tahmin 21 olsaydı: MAE 11 verirken MSE 121 verecektir. Dolayısıyla bu ikisinin de “hatanın cezalandırılması” hususunda ayrıştıklarını görüyoruz. Yani MSE’yi daha hassas, MAE’yi daha “toleranslı” olarak görebiliriz. Mesela siz bir linear regresyon yapıyorsunuz, bu ayrımı göz önüne alarak, "outlier"ları ne kadar göz ardı edeceğinize göre altta yatan metriği MSE veya MAE seçebilirsiniz. Varsayılanı "least squares"dir MSE’yi minimize eder; “least absolute deviations” olanı da MAE’yi.

Dolayısıyla, performans metriklerini seçerken gerek eldeki veriyi gerek de nihai amacı göz önünde bulundurmak gerekir. Metriklerin formülleri de bu değerlendirmelerde yararlı olur.

Yapıyor evet, sklearn genel olarak iki seriyi de _check_reg_targets’ten geçiriyor ve reshape(-1, 1) ile hizaya geliyorlar. Şöyle ya da böyle aynı sayıda sample’a sahip array-like olsalar yetiyor.

onurkizilarsan · Ağustos 18, 2021, 1:47öö

Çok teşekkür ederim gerçekten çok detaylı yazmışsınız. Ben bu projemde sıfır ve sıfıra yakın değerlere sahibim.

array([[0.   ],
       [0.003],
       [0.007],
       [0.008],
       [0.007],
       [0.007],
       [0.008],
       [0.007],
       [0.007],
       [0.008],

Bu da aslında sklearn sitesinde de belirttiği ve sizin de yukarıda açıkladığınız gibi büyük MAPE değerlerine sebep oluyor.

But note the fact that bad predictions can lead to arbitarily large MAPE values, especially if some y_true values are very close to zero. Note that we return a large value instead of when y_true is zero.inf

Bu yüzden ben hata metrikleri ile çalışacaksam her zaman MSE, MAE, RMSE, MAPE vs diye değil o çalışmamda hangi hata metriğine ihtiyacım varsa onu seçmem gerekiyor.

Aslında amacım, MSE, RMSE, MAE, MAPE ve diğer metrikleri uygulamalı olarak öğrenmek. Her birini denemeye çalışıyorum. Ancak MAPE metriğinde birden değerler fırlayınca ne olduğunu anlayamadım.

Bu projemde, elimdeki değerlerin Sıfır ve Sıfıra yakın olduğunu görüyorum ancak MAPE’nin buna uygun bir metrik olduğunu bilmediğim için yanlışlıkla kullandım. Aslında MAPE bu projemde yer almamalı. Acaba doğru anlamış mıyım?

FeRTeK · Ağustos 18, 2021, 5:42öö

Burada ki bilgiler işinize yarayabilir. sMAPE belki sizin tahminleme doğruluğunu ölçmek için model olabilir.

anon18277073 · Ağustos 18, 2021, 6:36öö

Doğrudur. Zamana bağlı seriler üzerinde kullanılan metrikler için şuraya bakabilirsiniz: https://otexts.com/fpp3/accuracy.html#accuracy. Örneğin MAPE’nin kullanımına dikkat edilmesi gerektiği söyleniyor, sMAPE’nin ise kullanılmaması tavsiye ediliyor.

onurkizilarsan · Ağustos 19, 2021, 11:36ös

Çok teşekkür ederim arkadaşlar sağolun @anon18277073 @aib @FeRTeK