Merhaba arkadaşlar ,
elimde şu şekilde bir denklem var : y(n) = 3.87y(n-1)(1-y(n-1)
bu denklemi çözebilmek için şu şekilde bir modülüm var : ym(n) = p * ym(n-1)*(1-ym(n-1))
bu denklemin eror’unu bulmak için : f = f + 1/n *(y(n)-ym(n))^2 ;
ayrıca f = 0 , y(0)=0.5 ve n = 1 den 300 kadar olduğunu söylenmekte.
burada benden yapılması istenen python’da curve fitting ve least_square yöntemi ile optimal p değerini bulmamız istenmektedir. Ayrıca alt tarafta yazdığım kod ise bu denklemin matlab programındaki yazılışıdır fakat bir türlü python’da yazmaya çalışırken başarılı olamıyorum bu konuda yardım edebilecek arkadaşların yardımını bekliyorum teşekkürler.
(https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.least_squares.html) burada least_square hakkında bilgi bulunmaktadır.
Matlab’ taki yazılımı :
p0 = 3.9
p = fminsearch(@objectivefunction,p0,options)
function [ f ] =objecivefunction§
ym(1) = 0.5 ;
y(1) = 0.5 ;
f = 0 ;
-
for n = 2 : 300, y(n) = 3.87*y(n-1)*(1-y(n-1) ; ym(n) = p *ym(n-1)*(1-ym(n-1)) ; f = f + 1/300 *(y(n)-ym(n)) ^2 ; end
end
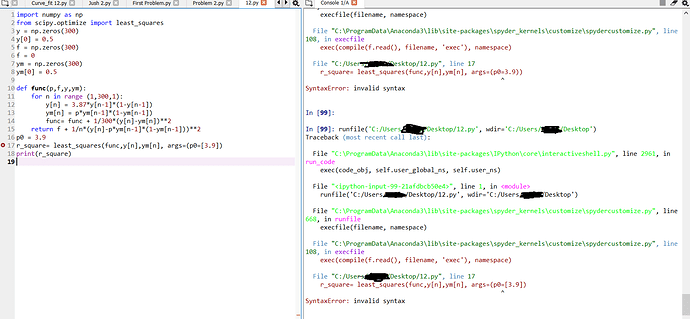
( Bu gördüğünüz ise benim python’da tanımlatmaya çalıştığım hali fakat hata veriyor. teşekkür ederim)
import numpy as np
from scipy.optimize import least_squares
y = np.zeros(300)
y[0] = 0.5
f = np.zeros(300)
f = 0
ym = np.zeros(300)
ym[0] = 0.5
def func(p,f,y,ym):
- for n in range (1,300,1):
> y[n] = 3.87y[n-1](1-y[n-1])
> ym[n] = pym[n-1](1-ym[n-1])
> func= func + 1/300*(y[n]-ym[n])*2
return f + 1/n(y[n]-pym[n-1](1-ym[n-1]))**2
p0 = 3.9
r_square= least_squares(func,y,ym, args=p0)
print(r_square)
