İstatistik bilgisi olan arkadaşlar var mı?

dildeolupbiten · Ekim 4, 2019, 7:06ös

Binom dağılımı, cohen’in kappa katsayısı gibi istatistik konularında bilgisi olan arkadaşlar var mı?

dildeolupbiten · Nisan 17, 2023, 10:21ös

Herkese merhaba,

Binom açılımıyla ve genel olarak terim açılımlarıyla alakalı biraz daha ayrıntıya girelim isterseniz.

Lise yıllarından hatırlayacağımız gibi binom açılımı, iki terimlinin toplamının üslü ifadesinin cebirsel açılımıdır ve bu teoremin genel yapısı (x + y)ⁿ şeklindedir.

Binom açılımındaki katsayılar şöyleydi hatırlarsanız:

[1]
[1, 1]
[1, 2, 1]
[1, 3, 3, 1]
[1, 4, 6, 4, 1]

Bu katsayılar aslında aşağıdaki olasılıkları da oluşturmaktadır:

[1.0]
[0.5, 0.5]
[0.25, 0.5, 0.25]
[0.125, 0.375, 0.375, 0.125]
[0.0625, 0.25, 0.375, 0.25, 0.0625]

Bu sayıları şu şekilde gösterirsek her halde daha iyi anlaşılırlar:

[1]
[1/2, 1/2]
[1/4, 2/4, 1/4]
[1/8, 3/8, 3/8, 1/8]
[1/16, 4/16, 6/16, 4/16, 1/16]

Gördüğünüz gibi binom açılımının katsayılarını aslında binom oranlarının pay kısmında görebiliyoruz, payda kısmında da terim sayısının açılma kuvvetleri yer alır.

Şimdi sizlerle bir fonksiyon yazacağız, bu fonksiyon, (x + y)ⁿ cebirsel ifadesinin açılımındaki katsayıları hesaplayacak. Bu katsayıları hesaplamak demek o katsayıyla alakalı olasılığı bulmak demektir aslında. Bu olasılığa da binom olasılığı denir.

Ve genel formülü şu şekildedir:

f(n, p, k) = n! / (k! * (n - k)!) * p^k * (1 - p)^{(n - k)}

Şimdi gelin bu formülü Python dilinde yazalım:

Önce bir factorial fonksiyonuna ihtiyacımız var. math.factorial işimizi görür ama math'te yer alan başka bir fonksiyonu tanıtmak için factorial hesabımızda ve ilerleyen hesaplamalarda bu fonksiyonu kullanacağım.

Evet factorial fonksiyonumuz şöyle:

from math import prod


def factorial(n: int) -> int:
    return prod(range(1, n + 1))

Şimdi de kombinasyon fonksiyonumuzu yazalım:

def combination(n: int, k: int) -> float:
    return factorial(n) / (factorial(k) * factorial(n - k))

Evet, ana fonksiyonumuzda ihtiyaç duyacağımız elemanları tanımladık. Şimdi yukarda verdiğim f fonksiyonunu tanımlayabiliriz. Bu fonksiyonun adına binomial_probability diyeceğim.

def binomial_probability(n: int, k: int, p: float) -> float:
    return combination(n, k) * p ** k * (1 - p) ** (n - k)

Şimdi bu fonksiyonu aşağıda gibi çağırıyorum:

for i in range(5):
    print([binomial_probability(n=i, k=j, p=1/2) for j in range(i + 1)])

Aldığım çıktı şöyle oluyor:

[1.0]
[0.5, 0.5]
[0.25, 0.5, 0.25]
[0.125, 0.375, 0.375, 0.125]
[0.0625, 0.25, 0.375, 0.25, 0.0625]

Gördüğünüz gibi, yukardaki fonksiyonlar iki terimli ifadelerin n. kuvvetlerinin katsayılarını hesaplıyor. Peki biz açılımı binom yani iki terimli değil de trinom veya tetranom veya pentanom isteseydik ne yapmamız gerekirdi?

Şimdi, gelin yukardaki fonksiyonlar üzerinde değişiklikler yapıp çok terimli ifadeler için kullanılabilir hale getirelim.

Binom olasılığında bir değişken, x olasılığında gerçekleştiğinde, diğer değişken ise 1-x olasılıkla gerçekleşir.

n = 3 durumunda iken x ve y’lerin alabileceği int değerler ne olabilir mesela?

x = 0 iken y = 3
x = 1 iken y = 2
x = 2 iken y = 1
x = 3 iken y = 0

Eğer biz trinom bir açılımdan bahsediyorsak, n = 3 durumunda şöyle değerlerimiz olmalıdır:

x = 0 iken, y = 0, z = 3
x = 0 iken, y = 1, z = 2
x = 0 iken, y = 3, z = 0
…

Şimdi, biz yukardaki fonksiyonlarda öyle bir algoritma değişikliği yapmalıyız ki, fonksiyonumuz multinomial olasılıkları hesaplamaya yatkın hale gelsin.

Ama öncelikle, binom açılımının formülüne tekrar bakalım:

f(n, p, k) = n! / (k! * (n - k)!) * p^k * (1 - p)^{(n - k)}

Gördüğünüz gibi burada k'yı parametre olarak vermiş olmamıza rağmen, ikinci değişkenin alacağı değerin ne olacağını açıkça belirtmemişiz, yerine n - k yazmışız. Oysa buna k₂ diyebilirdik. (1 - p) ifadesi de p₂ olabilirdi. Fonksiyonumuzu da şöyle yazabilirdik:

f(n, p, k) = n! / (k₁! * k₂!) * p₁^k₁ * p₂^k₂

Dolayısıyla 2 terimli için genel formül yukardaki gibi olurdu. Peki r terimli bir formülü şöyle yazamaz mıyız?

f(n, p, k) = n! / (k₁! * k₂! * … * k_r!) * p₁^k₁ * p₂^k₂ * … * p_r^k_r

O halde combination fonksiyonu yerine multicomb isminde yeni bir fonksiyon yazıyorum:

def multicomb(n: int, k: list) -> float:
    return factorial(n) / prod(map(factorial, k))

binomial_probability yerine multinomial_probability fonksiyonu yazmam gerekiyor. Onu da şöyle yazıyorum:

def multinomial_probability(n: int, k: list, p: list) -> float:
    return multicomb(n, k) * prod(map(pow, p, k))

Şimdi geldik, n terimli ifadelerin alabileceği olası k değerlerini hesaplamaya:

Normalde, binomial için, k1 ve k2 değerleri şöyle değerler alır.

n = 0 durumunda: [0, 0]
n = 1 durumunda: [[1, 0], [0, 1]
n = 2 durumunda: [[1, 1], [2, 0], [0, 2]]

Yani, k1 ve k2'nin toplamı n'in değerini geçemez.

Peki, biz [k1, k2, k3] listesindeki k’ları veya gerektiğinde [k1, k2, k3, k4] listesindeki k’ları hesaplamak için nasıl bir yöntem izleriz?

İki değişkenin alacağı değerleri şöyle kontrol edebiliriz:

[[i, n-i] for i in range(n + 1)]

Ama terim sayımıza duyarlı bir k değeri üreteci geliştirmemiz gerekiyor.

Üç terim için şöyle olabilir mi mesela?

[m, i - m, n - i] for i in range(n + 1) for m in range(i + 1)]

İyi ama terim sayımızı çoğalttıkça sürekli for döngüsü mü ekleyeceğiz koda? Bir de filtrelenmemiş bir liste bu. Üretilecek [k1, k2, k3] listelerinden k1 + k2 + k3 = n durumunu sağlayan itemler lazım.

Bunun için aşağıdaki algoritmayı yazdım. Bu algoritma, itertools.product gibi kartezyen ürünler üretiyor ama ondan farklı olarak kötü ürünleri de filtreliyor. (Kötü ürünler, toplamı açılma derecesini vermeyen ürünlerdir. Yukarda ne demiştik? k1 ve k2’nin toplamı n'in değerini geçemez. Yani, toplamı n sayısını geçen [k1, k2] çiftleri dağılıma ait değildir.) Fonksiyonun ismine k_values ismini veriyorum.

def k_values(n: int, r: int, stop: int = 0) -> list:
    return (
        [
            v for k in k_values(n, r - 1, stop + 1) for i in range(n + 1)
            if len(v := [i, *k]) != r + stop or sum(v) == n
        ]
        if r else [[]]
    )

k_values, fonksiyonundaki if len(v := [i, *c]) != r + stop or sum(v) == n ifadesi, product üzerinde filtreme yapmaya yarıyor. Bu ifade olmasaydı, itertools.product'ın üreteceği çıktının aynısı farklı bir algoritma ile üretilmiş olurdu.

Şimd, k_values'un 2 terimli olarak nasıl sonuçlar üreteceğine bir bakalım:

for i in range(5):
    print(k_values(n=i, r=2))

Aldığım sonuç:

[[0, 0]]
[[1, 0], [0, 1]]
[[2, 0], [1, 1], [0, 2]]
[[3, 0], [2, 1], [1, 2], [0, 3]]
[[4, 0], [3, 1], [2, 2], [1, 3], [0, 4]]

3 terimli için nasıl bir sonuç alıyoruz?

for i in range(5):
    print(k_values(n=i, r=3))

Çıktı:

[[0, 0, 0]]
[[1, 0, 0], [0, 1, 0], [0, 0, 1]]
[[2, 0, 0], [1, 1, 0], [0, 2, 0], [1, 0, 1], [0, 1, 1], [0, 0, 2]]
[[3, 0, 0], [2, 1, 0], [1, 2, 0], [0, 3, 0], [2, 0, 1], [1, 1, 1], [0, 2, 1], [1, 0, 2], [0, 1, 2], [0, 0, 3]]
[[4, 0, 0], [3, 1, 0], [2, 2, 0], [1, 3, 0], [0, 4, 0], [3, 0, 1], [2, 1, 1], [1, 2, 1], [0, 3, 1], [2, 0, 2], [1, 1, 2], [0, 2, 2], [1, 0, 3], [0, 1, 3], [0, 0, 4]]

Şimdi, her şeyi oluşturduğumuza göre, multinomial_probability fonksiyonumuzu çağırabiliriz:

Önce iki terimli dağılım ((a + b)ⁿ) için çağırıyorum.

for i in range(5):
    print([multinomial_probability(n=i, p=[1/2, 1/2], k=k) for k in k_values(n=i, r=2)])

Aldığım çıktı:

[1.0]
[0.5, 0.5]
[0.25, 0.5, 0.25]
[0.125, 0.375, 0.375, 0.125]
[0.0625, 0.25, 0.375, 0.25, 0.0625]

Gördüğünüz gibi, binomial_probability fonksiyonunun ürettiği çıktılarla aynı çıktıları aldık.

Şimdi de üç terimli dağılım ((a + b + c)ⁿ) için fonksiyonu çağırıyorum:

for i in range(5):
    print([multinomial_probability(n=i, p=[1/3, 1/3, 1/3], k=k) for k in k_values(n=i, r=3)])

Aldığım çıktı da şöyle oluyor:

[1.0]
[0.3333333333333333, 0.3333333333333333, 0.3333333333333333]
[0.1111111111111111, 0.2222222222222222, 0.1111111111111111, 0.2222222222222222, 0.2222222222222222, 0.1111111111111111]
[0.03703703703703703, 0.1111111111111111, 0.1111111111111111, 0.03703703703703703, 0.1111111111111111, 0.2222222222222222, 0.1111111111111111, 0.1111111111111111, 0.1111111111111111, 0.03703703703703703]
[0.012345679012345677, 0.0493827160493827, 0.07407407407407407, 0.0493827160493827, 0.012345679012345677, 0.0493827160493827, 0.14814814814814814, 0.14814814814814814, 0.0493827160493827, 0.07407407407407407, 0.14814814814814814, 0.07407407407407407, 0.0493827160493827, 0.0493827160493827, 0.012345679012345677]

Evet, algoritmamız çok terimli denklemlerin bütün sıralarının katsayılarını yani olasılık değerlerini hesaplıyor.

Bu olasılıklar ne işimize yarıyor diye merak eden arkadaşlarımız varsa söyleyeyim.

Hilesiz bir madeni parayı 100 kez yuvarladığımızda 70 yazı 30 tura şeklinde bir sonucun oluşma ihtimalini merak ediyorsak binom olasılığını kullanmak zorundayız.

Veya bir seçimde A adayı oyların %50’sini, B adayı %24’ünü ve C adayı da %'26’sını alıyor olsun. Rastgele 5 seçmen seçilirse, A adayı için 1, B adayı için 1 ve C adayı için 3 destekçi çıkma olasılığının ne olduğunu merak ediyorsak bunun için trinom (üç terimli) olasılığını kullanmak zorundayız.

Herkese iyi günler.

makesamba · Nisan 18, 2023, 9:04öö

üniversitede istatistikten çok acı çekmiştim. binom açılımı vs. tekrar görünce vietnam flashback yaşadım. küçük de bi antrenman oldu. teşekkürler elinize sağlık.

dildeolupbiten · Nisan 18, 2023, 10:18öö

Rica ederim, izninizle ek bir açıklama daha yapayım:

Buradaki ifade aslında yanıltıcı olabilir.

Binom açılımında iki terim vardır evet ama binom dağılımı, normal (gauss) dağılım ile aynı şey değildir.

k1 hangi değeri alırsa, k2 n - k1 değerini alabilir. Ve p1 hangi değeri alırsa, p2 de 1 - p1 değerini alır.

Burada p1 ve p2 olasılıklarının eşit olması bize normal bir dağılımı yani gauss dağılımını verirken, p1 ile p2’nin farklı olması durumunda da, binom dağılımını elde ederiz.

Aşağıdaki kodu çalıştırıp oluşan dağılımın farkına bakalım:

import matplotlib.pyplot as plt

n = 100

gauss_dist = [multinomial_probability(n=n, p=[1/2, 1/2], k=k) for k in k_values(n=n, r=2)]
binomial_dist1 = [multinomial_probability(n=n, p=[1/3, 2/3], k=k) for k in k_values(n=n, r=2)]
binomial_dist2 = [multinomial_probability(n=n, p=[2/3, 1/3], k=k) for k in k_values(n=n, r=2)]

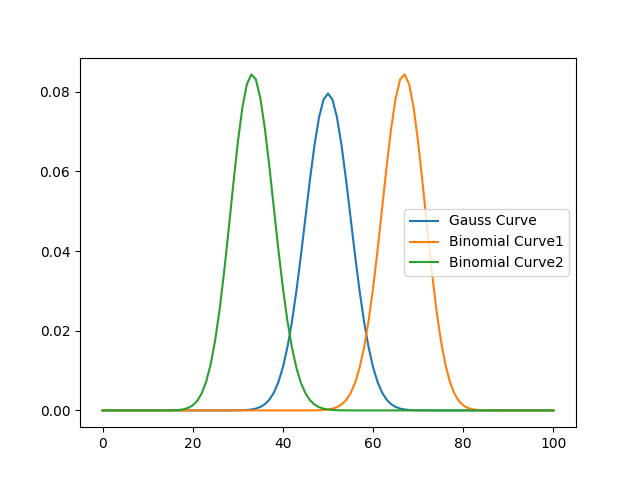
plt.plot(range(n + 1), gauss_dist, label="Gauss Curve")
plt.plot(range(n + 1), binomial_dist1, label="Binomial Curve1")
plt.plot(range(n + 1), binomial_dist2, label="Binomial Curve2")
plt.legend()
plt.show()

Figure_1

Yukardaki grafikte, normal dağılım ile binom dağılımının farkını görüyoruz.

Üç terimli cebirsel ifadeler için iki dağılımı karşılaştıralım:

import matplotlib.pyplot as plt

n = 100

dist1 = [multinomial_probability(n=n, p=[1/3, 1/3, 1/3], k=k) for k in k_values(n=n, r=3)]
dist2 = [multinomial_probability(n=n, p=[0.2, 0.3, 0.5], k=k) for k in k_values(n=n, r=3)]

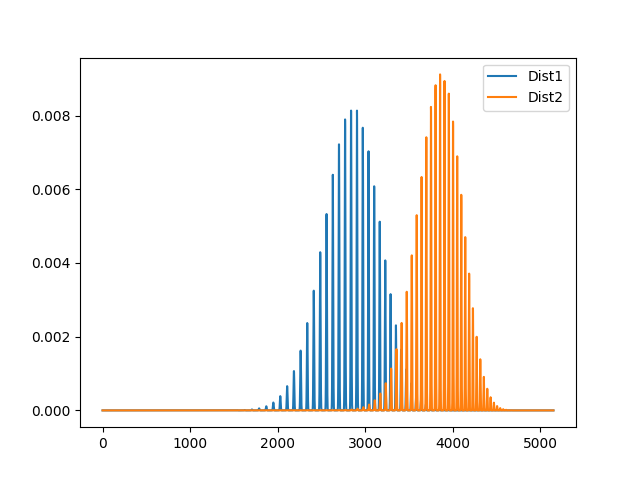
plt.plot(range(len(dist1)), dist1, label="Dist1")
plt.plot(range(len(dist2)), dist2, label="Dist2")
plt.legend()
plt.show()

Şöyle bir grafik elde ediyoruz.
Figure_2
Dört terimli için deneyelim:

import matplotlib.pyplot as plt

n = 100

dist1 = [multinomial_probability(n=n, p=[1/4, 1/4, 1/4, 1/4], k=k) for k in k_values(n=n, r=4)]
dist2 = [multinomial_probability(n=n, p=[0.2, 0.3, 0.1, 0.4], k=k) for k in k_values(n=n, r=4)]

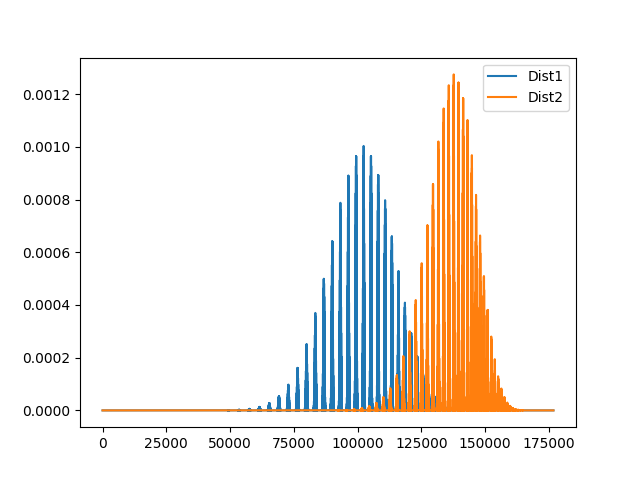
plt.plot(range(len(dist1)), dist1, label="Dist1")
plt.plot(range(len(dist2)), dist2, label="Dist2")
plt.legend()
plt.show()

4 terimli için n = 100 ifadesi biraz zaman alan bir işlem. Ama şöyle bir grafik elde ediyoruz:
Bu arada bu dağılımlar bu çözünürlükte göründükleri gibi değiller, zoom yapınca gerçek yapısı ortaya çıkıyor.
Figure_3

İlk mesajda bahsettiğim Cohen’in yöntemi de binom dağılımı gösteren dağılımın normal dağılıma ne kadar benzeyip benzemediğini ölçen bir yaklaşım.

Şöyle düşünün:

Bir madeni para deneyini 100 kez tekrarlıyor olalım. Bizim 60 aldığımız dağılım, normal dağılım ile karşılaştırıldığında nereye düşüyor?

Normal beklentimiz, madeni para deneyinin her seferde 1/2 olasılıkla gerçekleştiği ve büyük sayılar yasasına göre de n sayısı artıkça, yazı ve turaların oranının 1’e yaklaşması gerekir. n ne kadar artarsa, oran 1’e o kadar yaklaşır.

O halde, bizim 60/100 aldığımız deneyi adeta bir p değeri gibi ele alırız.
O halde p1; 60/100, p2 de 40/100 olur. Bu dağılımın, p1 = 50/100, p2 = 50/100 dağılımına ne kadar benzer?

import matplotlib.pyplot as plt

n = 100

dist1 = [multinomial_probability(n=n, p=[1/2, 1/2], k=k) for k in k_values(n=n, r=2)]
dist2 = [multinomial_probability(n=n, p=[60/100, 40/100], k=k) for k in k_values(n=n, r=2)]

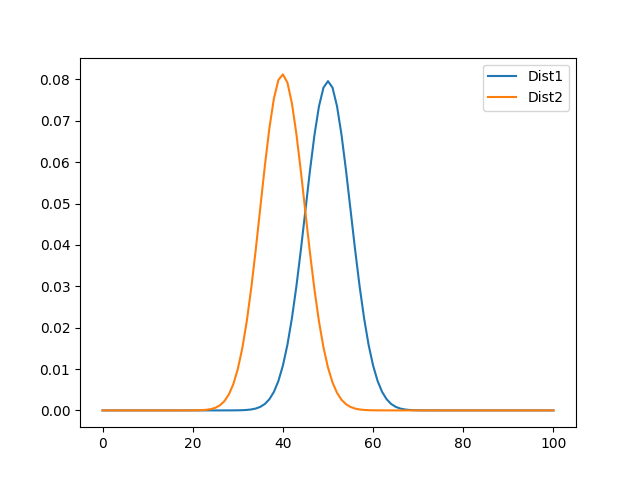
plt.plot(range(len(dist1)), dist1, label="Dist1")
plt.plot(range(len(dist2)), dist2, label="Dist2")
plt.legend()
plt.show()

Figure_4
Şimdi, burada dist2 dağılımının ortalamasının, dist1 dağılımında nereye düştüğü, bu olayın ne kadar sıklıkla gerçekleşebilecek bir olay olduğu ile ilgilidir. Binom dağılımı ne kadar gauss dağılımından uzaklaşırsa, o dağılımın gerçekleşme ihtimali de o kadar azalır (Ancak bir çok küçük ihtimal yeterli zaman içerisinde gerçekleşebilir.)

Shanyu · Nisan 18, 2023, 2:59ös

Acaba bütün dağılımlar, Merkezi Limit Teoremi gereği Normal Dağılıma ne kadar yaklaşırsa gerçekleşme oranı o kadar artar ve tersi durumda tersi olur mu, demek istiyoruz?.

dildeolupbiten · Nisan 18, 2023, 5:22ös

Şöyle anlatmaya çalışayım:

Bir madeni parayı tekrar tekrar 100 kere atıyoruz ve şu sonuçları alıyoruz:

n = 100
p = 1/2
k = 70

Oysa bizim beklediğimiz sonuç 50/50 gibi bir sonuçtu. Büyük sayılar yasası, n sayısı artıkça, k/n oranının p’ye yaklaşacağını söylüyor. Yani biz burada k’yı 70 aldık ama bu olayların her biri 1/2 olasılıkla gerçekleşiyor, dolayısıyla, n sayımız artıkça, n/k, p’ye daha çok yaklaşacak, dağılımımız normal dağılıma daha çok benzeyecektir. Ama gerçekleşme oranı 7/10 ve 3/10 olan iki terimli bir dağılım, n ne kadar artarsa artsın, normal dağılıma yaklaşamaz.

Burada kontrol grubumuz şöyle bir dağılım olsun:

n = 100
p = 1/2
k = 50

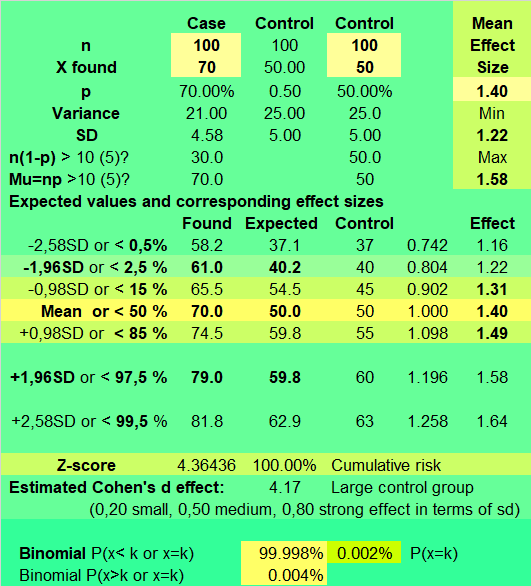
Bu iki dağılımı karşılaştırıyorum:

Buradaki Z-score değerine bakarsak, bu değer 70’in ortalamadan 4.36 standard sapma ötede yer aldığını gösteriyor. Bu şu demek, 70 sayısını ortalama etrafında dönen değerlerin % 99.99’unda bulamayacağız.

Bakın:

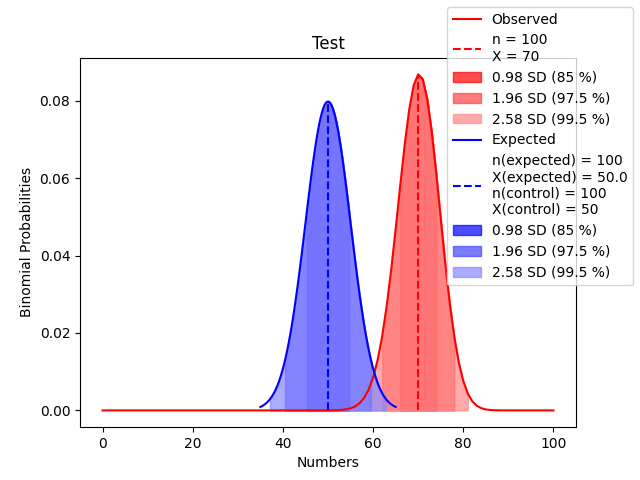
Teorik olarak 70 değeri, yaklaşık 78433 gün (217 sene) içinde denk gelebileceğimiz bir değer. 70 değerinin, mavi dağılımda nereye düştüğüne bakın. Bu iki dağılımın ortalamalarının arasındaki açıklıkla ilgili olan parametre de Cohen’in D etkisi oluyor. Bu değer 1 olduğunda, elimizdeki dağılım, beklenen dağılımdır.

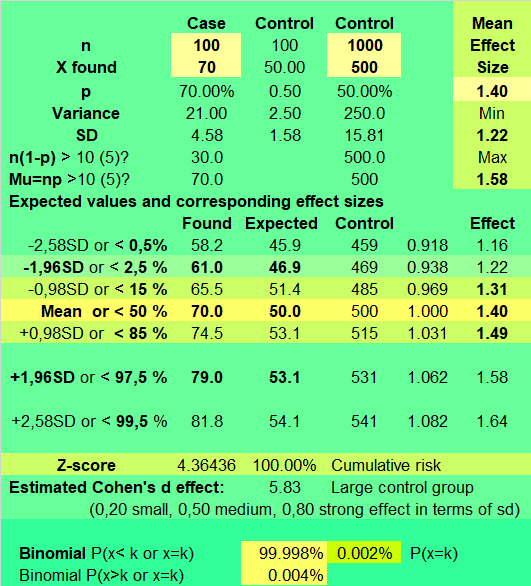
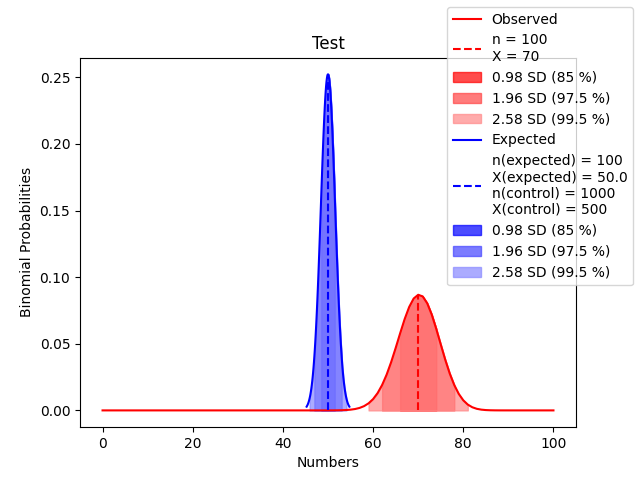
Kontrol grubunu büyütebiliriz tabi:

n = 1000
p = 1/2
k = 500

Bu kontrol grubuna göre kırmızı eğriyi, mavi eğriden daha uzakta görürüz. Ve n sayımız artıkça beklenen değerlerin dağılımını gösteren eğri de gitgide daralır ve uzar.

1/2 ihtimal üreten bir deney 100 kez tekrar edilirse 80/100 sonucu da alınabilir. Ama bu ihtimal mesela aşağı yukarı 46333333333 senede bir gerçekleşir. (Evrenin şu andaki yaşından uzun sürüyor gerçekleşmesi. )

dildeolupbiten · Nisan 19, 2023, 11:43öö

Yani şunu demeye çalışıyorum:

70/100’ün 50/100 karşısındaki durumu ile 700/1000’in 500/1000 karşısındaki durumu aynı değildir.

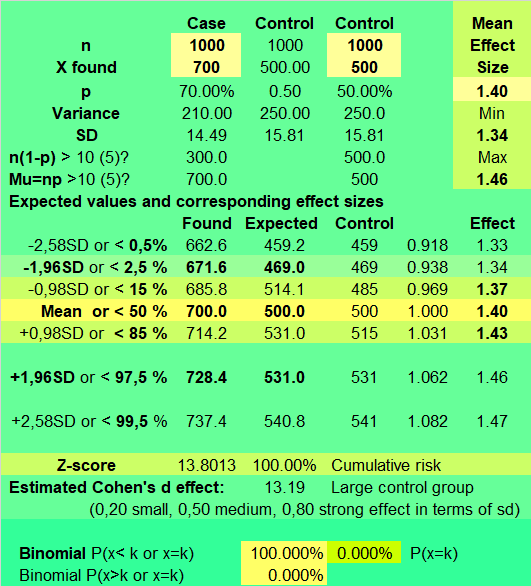
Şu durum: 700/1000’in 500/1000 karşısındaki durumu:

Burada, z-score 13.8 değerini alır. Yani 700, 500’den 13.8 standart sapma uzaktadır.

70/100 ile 50/100’ün durumuna bakalım:

Burada, z-score değerinin 4.36 olduğunu görüyoruz.

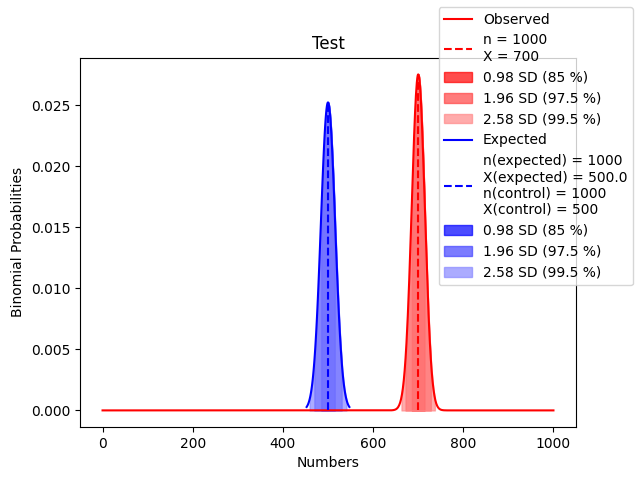
Dağılımlar da şöyle:

Dolayısıyla, eğer bir dağılım zaten normal bir dağılım değilse, n sayısını artırdığımızda, normal dağılım ile arasındaki z-score da giderek artacaktır.

Ama tesadüfen p=1/2 koşulu altında 70/100 sonucunu alıyorsak, buna şans denir. Ve n sayısı artıkça, oran 1/2’ye yaklaşır.

Ama baştan p1=7/10, p2=3/10 diye dağılımın oranlarını belirlersek, onun normal dağılıma yaklaşmayacağını, n sayısı artıkça, dağılımların giderek daha da ayrışmaya başlayacağını söyleyebiliriz.